Eckhard Limpert
and
Werner A. Stahel
Swiss Federal Institute of Technology Zurich
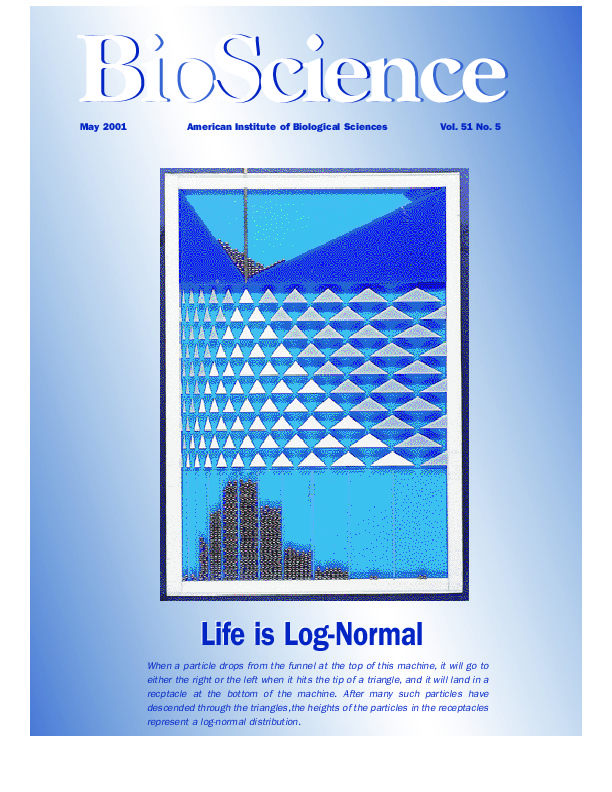
The figure at the cover page (Fig 1) provides a link between science and art and is not only interesting to look at. Moreover, it can lead to a deeper comprehension of frequency distributions that are important for life1,2. The figure shows a physical model for the distribution of particles that provides major clues to a better understanding of the distribution, for instance of:
Analogous to the well known Galton board3 for normal distributions, Fig. 1 demonstrates the genesis of a family of skewed, so-called lognormal distributions. The flow of particles falling from the funnel is deviated horizontally at each triangle in a particular, multiplicative way. If a triangle tip is at the horizontal position x, triangle tips to the right and to the left below it are placed at x times c and x divided by c (c = constant). At the same time, the model is a physical representation of the multiplicative central limit theorem in mathematical statistics. This theorem demonstrates how the lognormal distribution arises from many small, multiplicative random effects .
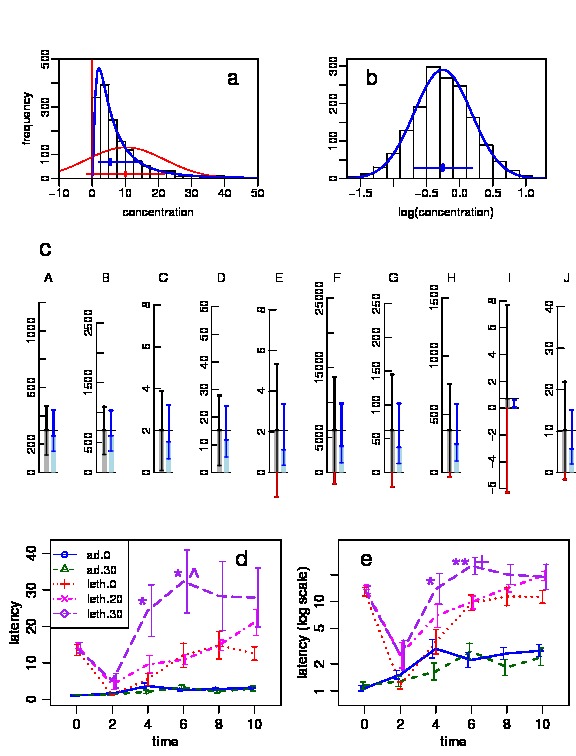
The comparison made in Fig. 2 offers a new way of characterizing lognormal data which is more informative than the established ways. Often, distributions are summarized by mean and standard deviation which is a poor description for skew distributions. If lognormal data are subjected to the log transformation (Fig. 2b), a normal distribution results, with mean mu and standard deviation sigma (e.g. 2,0.3). Back- transforming these values to the original scale gives the geometric mean4, mu*, and a standard deviation, sigma*, that is now multiplicative. These parameters (100,2) indicate that 68% of the distribution are within the range of 100 x/ 2 (100 times/divide 2), and 95% within 100 x/ 22.
Fig. 2 (below): Two ways of characterizing lognormal distributions, in terms of the original data (a) and after log-transformation (b). ... and more, see paper in plosOne
The quantities mu* and sigma* allow to characterize and compare lognormal data in terms of the original scale, which is preferred by most people. The multiplicative standard deviation sigma*, which determines the skewness of the distribution, is found to exhibit a typical value in many fields of applications.
Table 1: Ubiquity of lognormal distribution in life5,6
| Disciplines | mu* | sigma* | |
|---|---|---|---|
| Medicine | Onset of Alzheimer disease | ~ 60 years | 1.2 |
| Latent periods of infectious diseases | Hours to months | 1.5 | |
| Survival time after diagnosis of cancer | Months to years | 3 | |
| Environment | Air pollution in the U.S.A. | 40-110 PSI | 1.5-1.9 |
| Rainfall | 80-200 m3 (x103) | 4-5 | |
| Species abundance in ecology | - | 6-30 | |
| Social sciences and linguistics | Income of employed persons | 6.700sFr | 1.5 |
| Lengths of spoken words | 3-5 letters | 1.5 |
The model (Fig. 1), a computer application of which is in preparation, fills a 100 years old gap of demonstrating the genesis of these skewed distributions. Their characterization in terms of the original data makes complicated things easy, from science to various applications and everyday life. It's normal, that life is log-normal or - multiplicative normal .
Acknowledgements: The support from COST Switzerland and the Swiss Institute of Technology (ETH) is gratefully acknowledged.
Werner A. Stahel
is at the
Statistics Seminar
.
Swiss Federal Institute of Technology (ETH)
, CH-8092 Zurich, Switzerland.
E-mail addresses:
eckhard.limpert@bluewin.ch
werner.stahel@stat.math.ethz.ch
Copyright © E. Limpert ETH Zurich, 1988