Wahrscheinlichkeitsrechnung und Statistik
Über das Buch

Das Buch “Wahrscheinlichkeitsrechnung und Statistik” ist bei Springer erschienen.
Von der Buchrückseite:
Dieses Lehrbuch führt in die zentralen Begriffe und Konzepte der Wahrscheinlichkeitsrechnung, der beschreibenden sowie der schließenden Statistik ein. Der Fokus liegt dabei auf einem intuitiven Verständnis der grundlegenden Konzepte, Zusammenhänge und Methoden. Trotzdem wird der Stoff mathematisch präzise präsentiert. Innerhalb jedes Kapitels finden Sie verschiedene didaktische Elemente, die Ihnen den Zugang und das Verständnis, aber auch die Orientierung deutlich erleichtern:
- Kurzübersicht der wichtigsten Begriffe am Kapitelanfang
- Anschauliche Erklärungen und Beispiele
- Zentrale Sachverhalte und Definitionen
- Warnungen vor häufigen Missverständnissen
- Separate Textabschnitte zur Intuition
- Grafische oder tabellarische Übersichten am Kapitelende
Am Ende der meisten Abschnitte finden Sie kurze Lernkontrollen – hier können Sie Ihr Wissen überprüfen, indem Sie verschiedene Aussagen als wahr oder falsch einordnen. Die Lösungen finden Sie im Anhang, je nach Schwierigkeitsgrad mit kurzem Lösungsweg. Am Ende der Kapitel finden Sie außerdem Verständnisfragen, die noch einmal die wichtigsten Inhalte abfragen und so Ihren Lernfortschritt zeigen.
Feedback
Falls Sie Fehler gefunden haben, Fragen oder Feedback haben: Bitte per E-Mail melden. Alternativ kann auch eine anonyme Meldung via Formular gemacht werden. Besten Dank!
Errata
Hier verfügbar als PDF (Stand: 23. Mai 2022).
Zusammenfassungsblätter
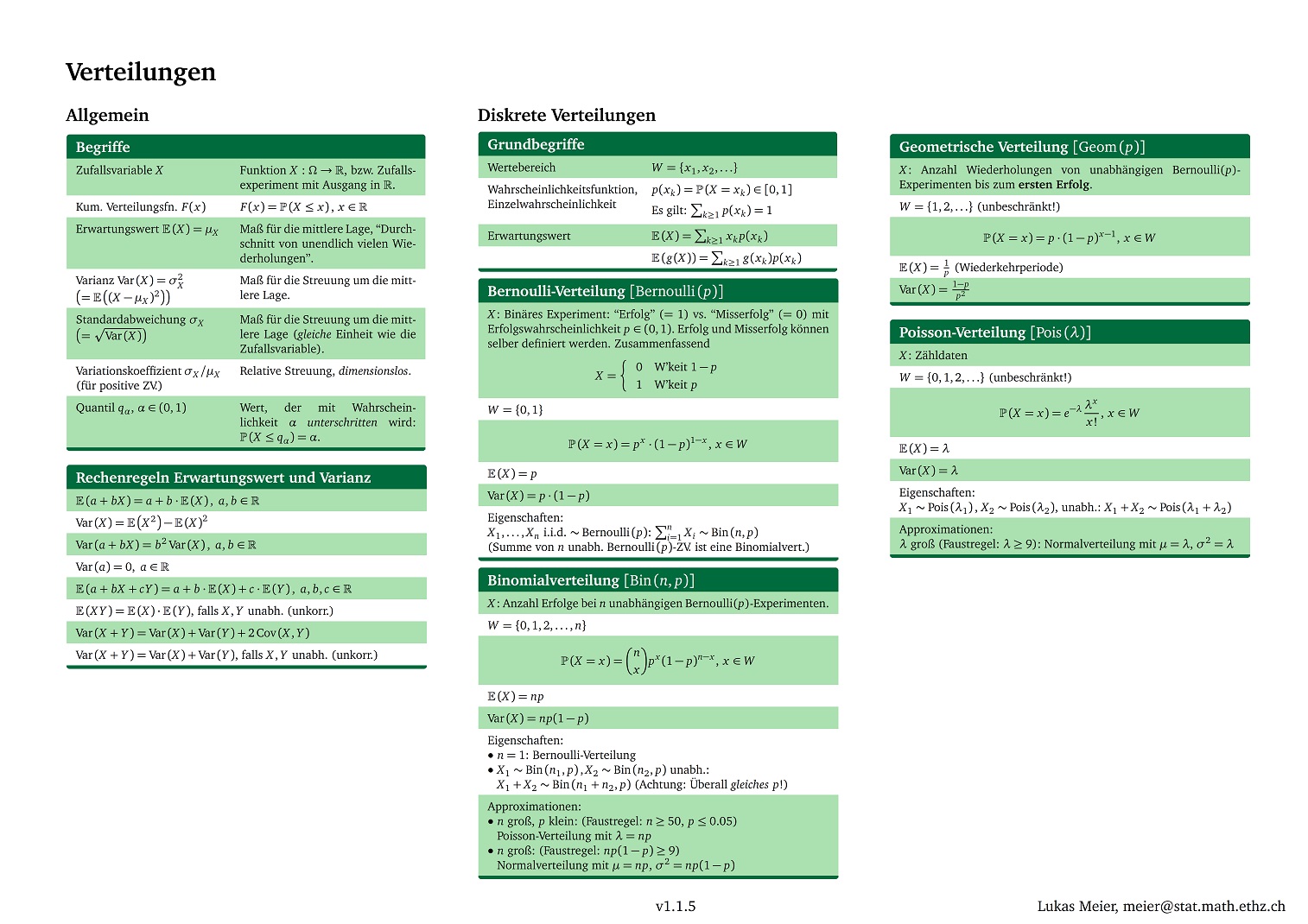
Folgende Zusammenfassungsblätter (“cheat sheets”) sind vorhanden:
| Grundlagen | Verteilungen | Statistik |
|---|---|---|
 |
  |
  |
| Download PDF | Download PDF | Download PDF |
Bemerkung: Die cheat sheets wurden mit diesem Template in Latex erstellt.
Interaktives
Macht (Power): Einseitiger Z-Test
Animation zur Illustration der Verteilung eines Schätzers.
R
Dieser Abschnitt soll illustrieren, wie die verschiedenen Methoden
und Beispiele im Buch in der Software R umgesetzt werden
können. Dieses Dokument ist keine R-Einführung, sondern soll
aufzeigen, wie R als “Taschenrechner” eingesetzt werden
kann, um die Beispiele im Buch nachzurechnen. Die Kapitel beziehen sich
jeweils auf die Nummerierung im Buch.
2 Wahrscheinlichkeitsverteilungen
Die verwendeten Funktionen haben alle denselben Aufbau. Die Bedeutung des Anfangsbuchstabens kann folgender Tabelle entnommen werden:
| Anfangsbuchstabe | Bedeutung |
|---|---|
d (density) |
Wahrscheinlichkeitsfunktion bzw. Dichte |
p (probabilty) |
Kumulative Verteilungsfunktion, d.h. \(\mathbb{P}(X \le x)\), bzw. \(\mathbb{P}(X > x)\) falls Argument
lower.tail = FALSE. |
q (quantile) |
Quantilsfunktion |
r (random) |
Zufallszahlen generieren |
Für die Verteilungen wird in R folgendes Namensschema
verwendet:
| Name | Verteilung |
|---|---|
binom |
Binomialverteilung (enthält Bernoulli-Verteilung) |
geom |
Geometrische Verteilung |
poisson |
Poisson-Verteilung |
unif |
Uniforme Verteilung |
norm |
Normalverteilung |
exp |
Exponentialverteilung |
So ist z.B. pbinom die kumulative Verteilungsfunktion
der Binomialverteilung.
2.2 Diskrete Verteilungen
2.2.2 Bernoulli-Verteilung
Die Bernoulli-Verteilung ist durch die Binomialverteilung mit \(n = 1\) implementiert.
2.2.3 Binomialverteilung
Die Wahrscheinlichkeitsfunktion der Binomialverteilung ist
dbinomial. Der Aufruf ist
dbinom(x, size, prob), wobei size der Anzahl
der Experimente \(n\) entspricht und
prob der jeweiligen Erfolgswahrscheinlichkeit \(p\). Für das Beispiel mit den Bauteilen
können wir die Resultate aus dem Buch folgendermaßen nachrechnen (es
gilt dort \(n = 10\) und \(p = 0.05\)).
\(\mathbb{P}(X = 3)\):
## [1] 0.01047506\(\mathbb{P}(X \ge 1)\):
## [1] 0.4012631Alternativ: \(\mathbb{P}(X \ge 1) = \mathbb{P}(X > 0)\):
## [1] 0.40126312.2.4 Geometrische Verteilung
Die Wahrscheinlichkeitsfunktion der geometrischen Verteilung ist
dgeom. Der Aufruf ist entsprechend
dgeom(x, prob), wobei zu beachten ist, dass die Verteilung
hier auf der Menge \(\{0, 1, 2,
\ldots\}\) definiert ist. D.h., die Wahrscheinlichkeit, gerade
beim ersten Mal Erfolg zu sehen, wäre dann dgeom(0, prob)
(wir müssen als unsere Werte um 1 verschieben!).
Für das Beispiel mit dem Jahrhundertereignis erhalten wir folgende Größen:
\(\mathbb{P}(X \le 50)\):
## [1] 0.3949939Das 50%-Quantil (Median!) erhalten wir mit:
## [1] 68Dies entspricht in unserer Sichtweise dem Wert 69.
2.2.5 Poisson-Verteilung
Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung ist
dpois. Der Aufruf ist dpois(x, lambda).
Für das Beispiel mit dem Callcenter (\(\lambda = 5\)) gibt dies folgende Resultate:
\(\mathbb{P}(X = 0)\):
## [1] 0.006737947\(\mathbb{P}(X = 5)\):
## [1] 0.1754674Beim überbuchten Flug (\(\lambda = 204 \cdot 0.05 = 10.2\)) ist die Rechnung folgendermaßen:
\(\mathbb{P}(X \ge 4) = \mathbb{P}(X > 3)\):
## [1] 0.9910759Oder exakt mit der Binomialverteilung:
## [1] 0.99222392.3 Stetige Verteilungen
2.3.3 Uniforme Verteilung
Die kumulative Verteilungsfunktion wird aufgerufen durch
punif(x, min, max), wobei min und
max den Werten \(a\) und
\(b\) im Buch entsprechen. Für das
Beispiel mit den Zufallszahlen erhalten wir:
\(\mathbb{P}(2 \le X \le 4)\):
## [1] 0.4## [1] 0.42.3.4 Normalverteilung
Bei der Normalverteilung ist der Funktionsaufruf von der Form
pnorm(x, mean, sd). Die Argumente sind also der
Erwartungswert und die Standardabweichung (nicht die Varianz!).
Für \(\mu = 3\) und \(\sigma = 4\) können wir das Beispiel bei
der Standardisierung direkt rechnen:
\(\mathbb{P}(X \le 3)\):
## [1] 0.5987063Quantile können wir mit der Funktion qnorm berechnen,
z.B. für die Standardnormalverteilung (\(z_{\alpha}\)) für \(\alpha = 0.9, 0.95, 0.975, 0.99,
0.995\):
## [1] 1.281552 1.644854 1.959964 2.326348 2.5758292.3.5 Exponentialverteilung
Bei der Exponentialverteilung ist der Funktionsaufruf von der Form
pexp(x, rate), d.h., der Parameter rate
entspricht dem Parameter \(\lambda\) im
Buch. Wir rechnen nach:
\(\mathbb{P}(T \le 10)\):
## [1] 0.4865829\(\mathbb{P}(T > 20)\):
## [1] 0.2635971\(\mathbb{P}(T \le 15)\):
## [1] 0.63212063 Deskriptive Statistik
3.2 Kennzahlen
Die wichtigsten Funktionen sind in folgender Tabelle aufgelistet:
| Funktion | Bedeutung |
|---|---|
mean |
Arithmetisches Mittel |
median |
Empirischer Median |
var |
Empirische Varianz |
sd |
Empirische Standardabweichung |
quantile |
Empirische Quantile (Achtung: verschiedene Definitionen!) |
Die Daten des Geysirs Old Faithful sind im Datensatz
faithful direkt in R vorhanden.
## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55
## 7 4.700 88
## 8 3.600 85
## 9 1.950 51
## 10 4.350 85## [1] 3.600 1.800 3.333 2.283 4.533 2.883 4.700 3.600 1.950 4.350Davon können wir nun diverse Kennzahlen berechnen:
## [1] 3.3032## [1] 1.11605## [1] 1.056433## [1] 3.4665## 15%
## 1.95## 25%
## 2.283## 75%
## 4.35## 75%
## 2.0673.3 Grafische Darstellungen
3.3.1 Histogramm
Ein Histogramm können wir in R mit der Funktion
hist erstellen. Die Anzahl der Klassen wird durch das
Argument breaks gesteuert (je nach Argumenttyp wird dieses
aber nur als “Vorschlag” interpretiert, siehe ?hist).
hist(faithful[, "waiting"], breaks = 10, xlab = "Zeitspanne (Minuten)",
main = "Histogramm der Zeitspannen zwischen Ausbrüchen")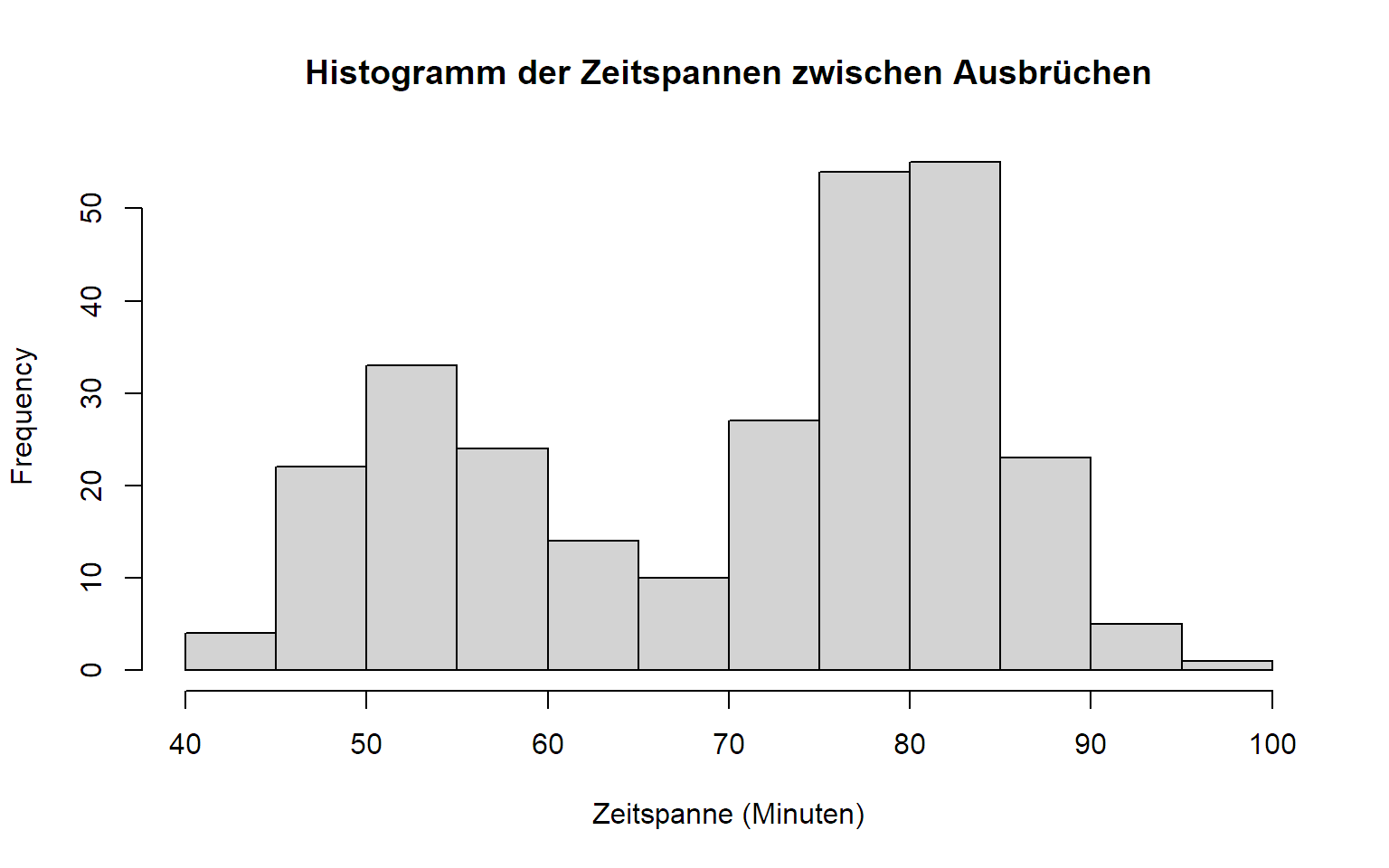
3.3.2 Boxplot
Einen Boxplot erstellt man in R mit der Funktion
boxplot.
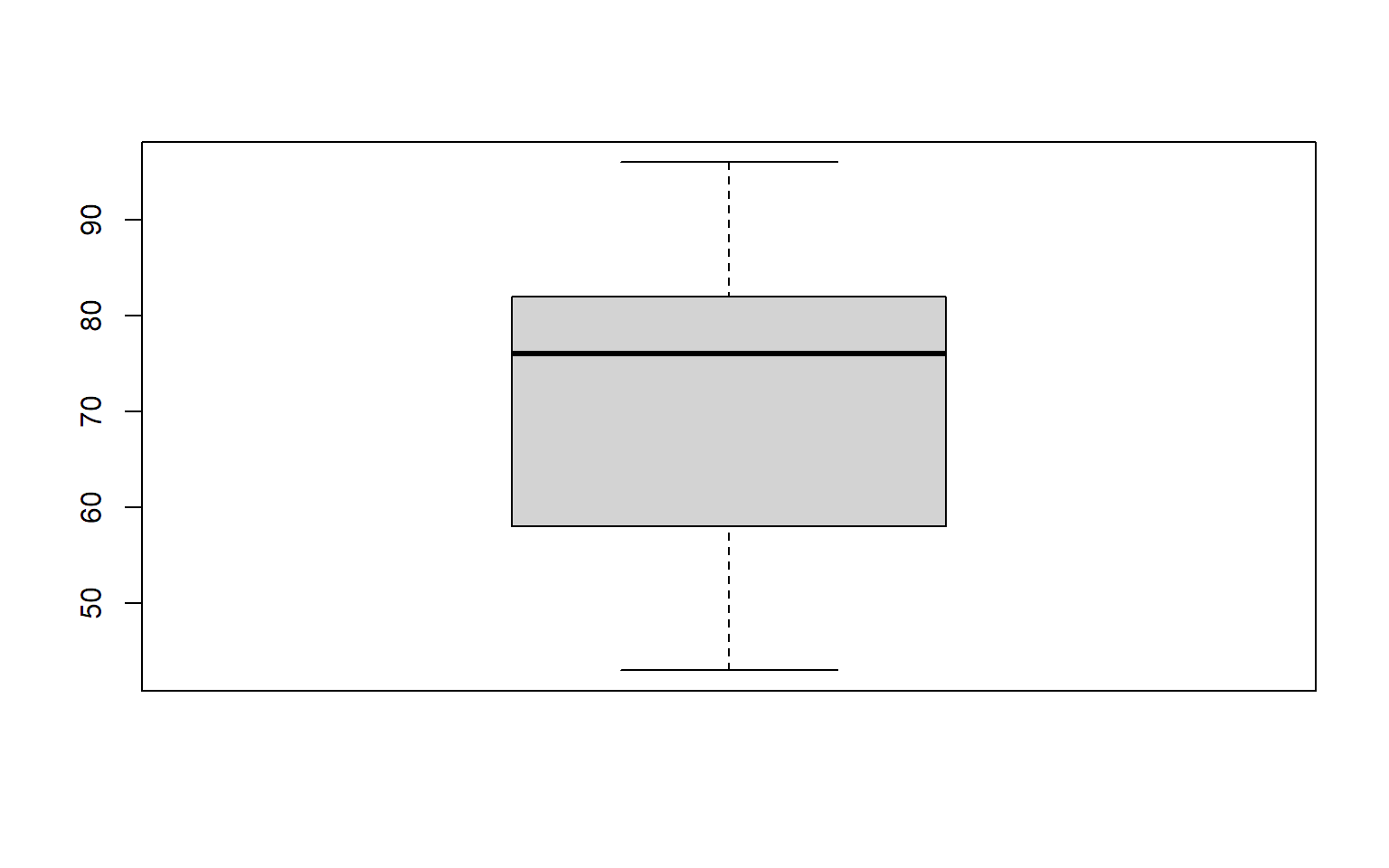
3.3.3 Empirische kumululative Verteilungsfunktion
Die empirische kumulative Verteilungsfunktion können wir mit der
Funktion ecdf erstellen. Wir erhalten so eine Funktion (!),
die wir an beliebigen stellen evaluieren können. Natürlich können wir
diese auch aufzeichnen.
## [1] 0.3051471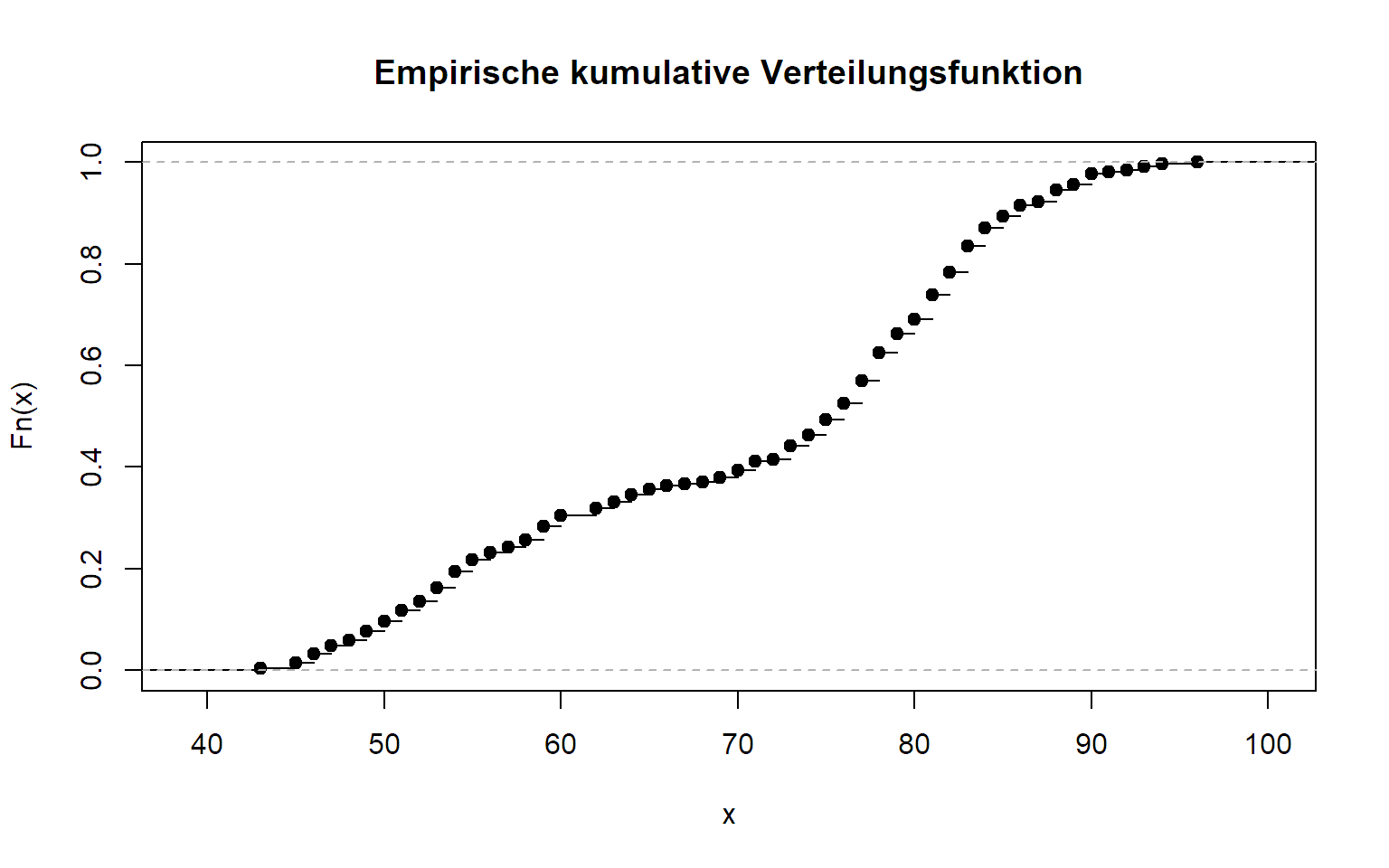
3.4 Mehrere Messgrößen
Ein Streudiagramm kann mit der Funktion plot erstellt
werden.
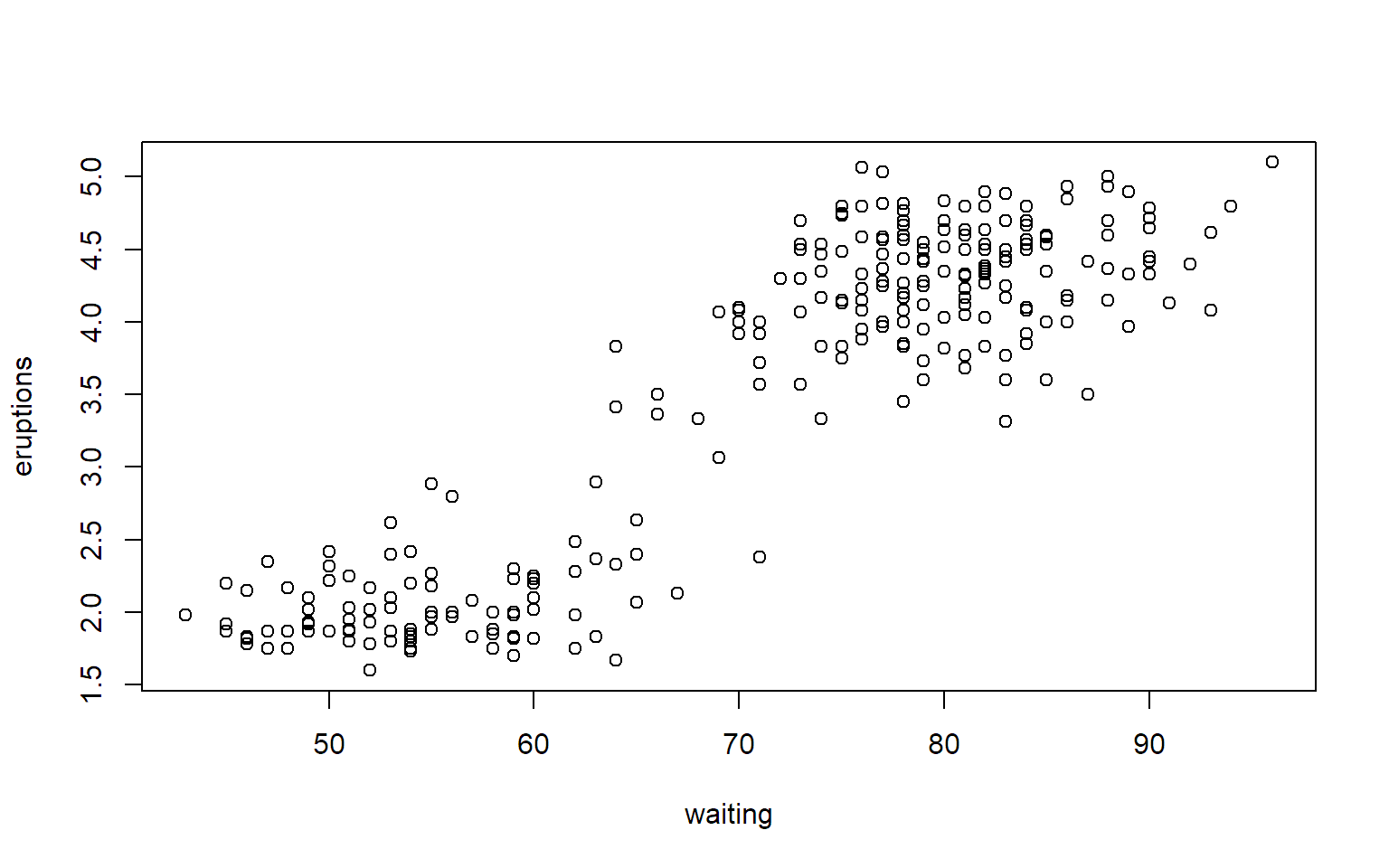
Bemerkung: Die entsprechende Abbildung im Buch wurde mit den Daten von http://stat.ethz.ch/Teaching/Datasets/geysir.dat erstellt.
Hinweis: Funktionen zur Berechnung von Kennzahlen:
| Funktion | Bedeutung |
|---|---|
cov |
Empirische Kovarianz |
cor |
Empirische Korrelation |
Zusatzmaterial
Wie beim Anscombe’s Quartet haben folgende Datensätze alle die gleichen arithmetischen Mittel, empirischen Standardabweichungen und empirische Korrelationen, siehe auch die Diskussion hier.
data(datasaurus_dozen, package = "datasauRus") ## enthält Daten
library(ggplot2) ## für den Plot
ggplot(datasaurus_dozen, aes(x = x, y = y)) + geom_point() + facet_wrap(~ dataset, ncol = 5)
Entsprechende Kennzahlen können wir hier mit etwas komplizierterem
R-Code für alle Gruppen berechnen:
myfun <- function(x) c("mean" = mean(x), "sd" = sd(x))
aggregate(. ~ dataset, data = datasaurus_dozen, myfun)## dataset x.mean x.sd y.mean y.sd
## 1 away 54.26610 16.76982 47.83472 26.93974
## 2 bullseye 54.26873 16.76924 47.83082 26.93573
## 3 circle 54.26732 16.76001 47.83772 26.93004
## 4 dino 54.26327 16.76514 47.83225 26.93540
## 5 dots 54.26030 16.76774 47.83983 26.93019
## 6 h_lines 54.26144 16.76590 47.83025 26.93988
## 7 high_lines 54.26881 16.76670 47.83545 26.94000
## 8 slant_down 54.26785 16.76676 47.83590 26.93610
## 9 slant_up 54.26588 16.76885 47.83150 26.93861
## 10 star 54.26734 16.76896 47.83955 26.93027
## 11 v_lines 54.26993 16.76996 47.83699 26.93768
## 12 wide_lines 54.26692 16.77000 47.83160 26.93790
## 13 x_shape 54.26015 16.76996 47.83972 26.93000## Oder "einzeln" mit folgendem auskommentiertem R-Code:
## aggregate(. ~ dataset, data = datasaurus_dozen, mean)
## aggregate(. ~ dataset, data = datasaurus_dozen, sd)Für die Korrelation geht dies mit einer Kombination von
split und sapply:
sapply(split(datasaurus_dozen[,c("x", "y")], datasaurus_dozen$dataset), function(m) cor(m[,1], m[,2]))## away bullseye circle dino dots h_lines
## -0.06412835 -0.06858639 -0.06834336 -0.06447185 -0.06034144 -0.06171484
## high_lines slant_down slant_up star v_lines wide_lines
## -0.06850422 -0.06897974 -0.06860921 -0.06296110 -0.06944557 -0.06657523
## x_shape
## -0.06558334Alternativ geht dies auch mit dem Paket dplyr:
## # A tibble: 13 × 2
## dataset correlation
## <chr> <dbl>
## 1 away -0.0641
## 2 bullseye -0.0686
## 3 circle -0.0683
## 4 dino -0.0645
## 5 dots -0.0603
## 6 h_lines -0.0617
## 7 high_lines -0.0685
## 8 slant_down -0.0690
## 9 slant_up -0.0686
## 10 star -0.0630
## 11 v_lines -0.0694
## 12 wide_lines -0.0666
## 13 x_shape -0.06566 Parameterschätzungen
6.2 Wahl der Verteilungsfamilie
In R kann mit der Funktion qqnorm ein
Normalplot erstellt werden. Der erste Plot in Abbildung 6.1a kann
folgendermaßen reproduziert werden:
x <- c(-2.21, -1.99, -1.47, -1.38, -0.84, -0.82, -0.71, -0.69, -0.63,
-0.62, -0.48, -0.41, -0.39, -0.31, -0.25, -0.16, -0.16, -0.11,
-0.1, -0.06, -0.06, -0.05, -0.04, -0.02, 0.07, 0.18, 0.33, 0.36,
0.39, 0.39, 0.42, 0.49, 0.56, 0.58, 0.59, 0.62, 0.7, 0.74, 0.76,
0.77, 0.78, 0.82, 0.88, 0.92, 0.94, 1.1, 1.12, 1.36, 1.51, 1.6)
qqnorm(x)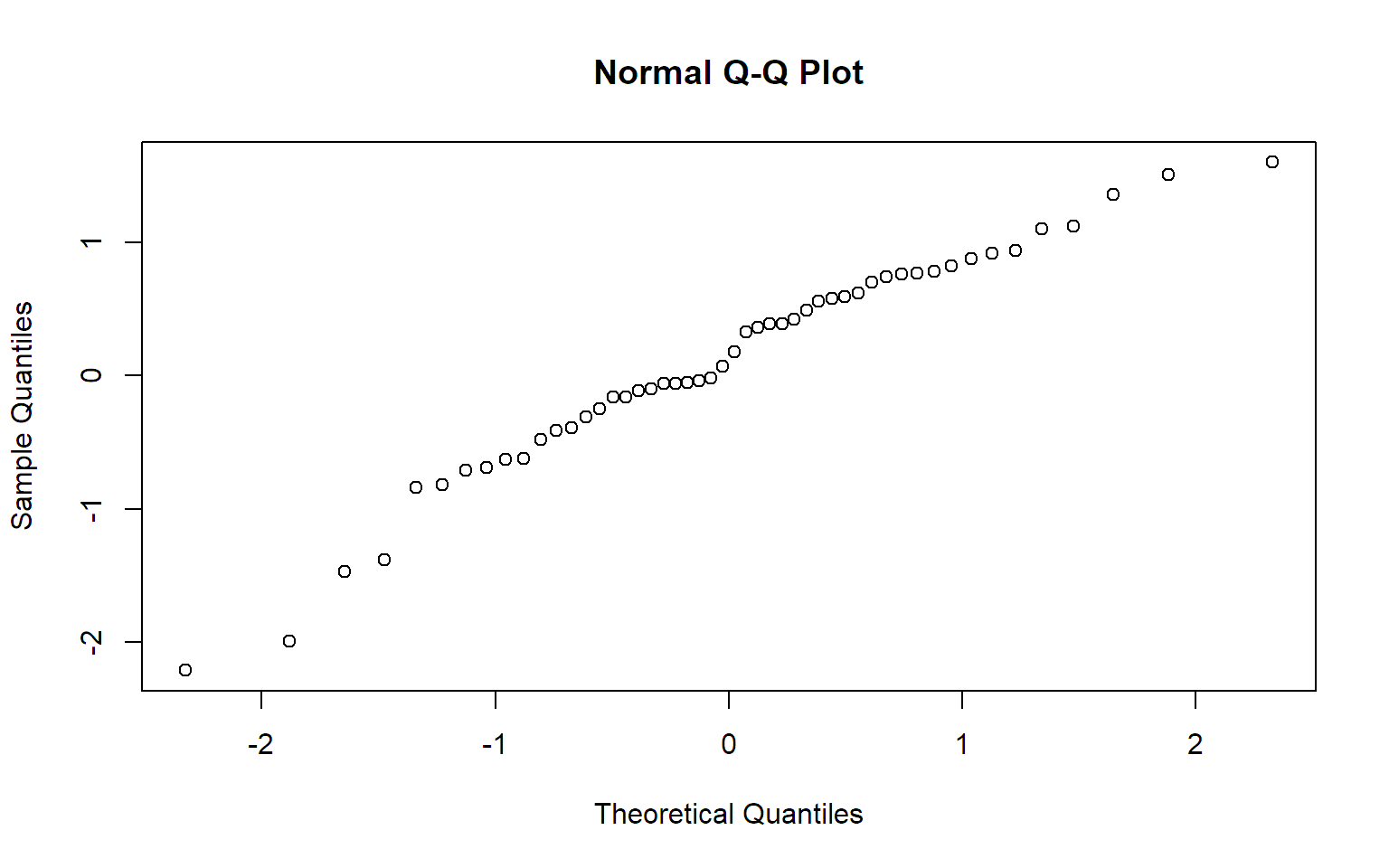
7 Statistische Tests und VI für eine Stichprobe
7.1 Einführung
7.1.1 Illustration: Binomialtest
Der Binomialtest ist in R in der Funktion
binom.test implementiert. Für das Beispiel mit den defekten
Bauteilen mit \[H_0: p = p_0 = 0.1\]
\[H_A: p > 0.1\] hatten wir die
Daten \(n = 20\) (Anzahl der Bauteile)
und \(x = 5\) (Anzahl der defekten
Bauteile). Die einseitige Alternative spezifizieren wir mit dem Argument
alternative = "greater".
##
## Exact binomial test
##
## data: 5 and 20
## number of successes = 5, number of trials = 20, p-value = 0.04317
## alternative hypothesis: true probability of success is greater than 0.1
## 95 percent confidence interval:
## 0.1040808 1.0000000
## sample estimates:
## probability of success
## 0.25Den Testentscheid lesen wir direkt am p-Wert ab
(p-value = 0.04317).
7.2 Tests für eine Stichprobe bei normalverteilten Daten
7.2.2 t-Test
Der \(t\)-Test ist in der Funktion
t.test implementiert. Die Nullhypothese kann mit dem
Argument mu spezifiziert werden. Die Richtung der
Alternativhypothese kann wieder mit dem Argument
alternative angegeben werden (standardmäßig wird zweiseitig
getestet).
Für das Beispiel mit der Abfüllmaschine erhalten wir:
machine <- c(1003.05, 1004.11, 1002.61, 1002.51, 1003.99, 1003.02,
1002.95, 1001.9, 999.7, 1002.47)
## Zur Kontrolle mit dem Buch: Berechnung des arithmetischen Mittels
## und der empirischen Standardabweichung der Daten.
mean(machine)## [1] 1002.631## [1] 1.230587##
## One Sample t-test
##
## data: machine
## t = 6.761, df = 9, p-value = 8.262e-05
## alternative hypothesis: true mean is not equal to 1000
## 95 percent confidence interval:
## 1001.751 1003.511
## sample estimates:
## mean of x
## 1002.631Anhand obigem Output sehen wir den Wert der Teststatistik
(t = 6.761), den p-Wert
(p-value = 8.262e-05) sowie das
95%-Vertrauensintervall für den Erwartungswert
(1001.751 1003.511).
7.3 Allgemeine Eigenschaften von statistischen Tests
7.3.1 Macht
Die Macht beim einseitigen Binomialtest \(H_0: p = p_0 = 0.5\) und \(H_A: p > 0.5\) berechnet sich für die Situation \(p = 0.75\) folgendermaßen (der Verwerfungsbereich ist in diesem Fall \(\{9,10\}\)).
## [1] 0.2440252Wie würde man einen solchen Fall mit einer Simulation lösen? Wir simulieren hierzu 1000 Mal von einer Binomialverteilung mit \(n = 10\) und \(p = 0.75\) und speichern den jeweiligen Testentscheid des Binomialtests. Dann schauen wir über alle Simulationen hinweg, wie oft verworfen wird. Diese relative Häufigkeit ist nichts anderes als eine Schätzung für die Wahrscheinlichkeit, dass man die Nullhypothese verwerfen kann, was genau der Macht entspricht.
set.seed(79) ## Zwecks Reproduzierbarkeit
n.sim <- 1000
results <- logical(n.sim) ## Zur Speicherung der Resultate
for(i in 1:n.sim){
x <- rbinom(1, size = 10, prob = 0.75) ## Simuliere unter Alternativhypothese p = 0.75
out <- binom.test(x, n = 10, p = 0.5, alternative = "greater")
results[i] <- out$p.value < 0.05 ## TRUE / FALSE (Wird verworfen? Ja oder nein?)
}
mean(results) ## Relative Häufigkeit der Fälle bei denen verworfen wird## [1] 0.248Wir sehen, dass wir mit einer solchen Simulation der richtigen Macht
0.244 schon nahe kommen. Für mehr Genauigkeit können wir einfach den
Wert von n.sim erhöhen. Wir können sogar schauen, wie genau
unsere simulationsbasierte Schätzung ist, indem wir einen Binomialtest
anwenden und dann das entsprechende Vertrauensintervall für die wahre
Erfolgswahrscheinlichkeit (die Macht!) ablesen. Der Grund liegt darin,
dass obige Simulation nichts anderes als n.sim unabhängige
Bernoulli-Experimente sind, wobei die Erfolgswahrscheinlichkeit durch
die Macht gegeben ist (welche wir schätzen wollen). Wir erhalten so:
##
## Exact binomial test
##
## data: sum(results) and length(results)
## number of successes = 248, number of trials = 1000, p-value < 2.2e-16
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.2215081 0.2759842
## sample estimates:
## probability of success
## 0.248In obigem Fall ist dies also \([0.22,
0.28]\). Wenn die Breite nicht den Anforderungen entspricht, kann
diese durch eine Erhöhung des Wertes für n.sim einfach
reduziert werden.
7.5 Tests für eine Stichprobe bei nicht normalvert. Daten
7.5.1 Vorzeichentest
Für den Vorzeichentest (der ja nichts anderes als ein Binomialtest
ist), können wir die Funktion binom.test verwenden.
machine <- c(1003.05, 1004.11, 1002.61, 1002.51, 1003.99, 1003.02,
1002.95, 1001.9, 999.7, 1002.47)
binom.test(sum(machine > 1000), n = length(machine), p = 0.5)##
## Exact binomial test
##
## data: sum(machine > 1000) and length(machine)
## number of successes = 9, number of trials = 10, p-value = 0.02148
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.5549839 0.9974714
## sample estimates:
## probability of success
## 0.9Wir erhalten den gleichen p-Wert (p-value = 0.02148) wie
im Buch.
7.5.2 Wilcoxon-Test
Den Wilcoxon-Test findet man in R in der Funktion
wilcox.test. Im Beispiel mit der Abfüllmaschine lautet der
Aufruf:
machine <- c(1003.05, 1004.11, 1002.61, 1002.51, 1003.99, 1003.02,
1002.95, 1001.9, 999.7, 1002.47)
wilcox.test(machine, mu = 1000)##
## Wilcoxon signed rank exact test
##
## data: machine
## V = 54, p-value = 0.003906
## alternative hypothesis: true location is not equal to 1000Der Wert der Teststatistik (V = 54) stimmt mit dem Wert
im Buch überein. Den Testentscheid können wir hier aber einfacher direkt
am p-Wert (p-value = 0.003906) ablesen.
8 Vergleich zweier Stichproben
8.3 Gepaarte Vergleiche
Mit dem Argument paired = TRUE kann mit der Funktion
t.test ein gepaarter t-Test durchgeführt werden. Für das
Beispiel mit den Übermittlungszeiten gibt dies:
x <- c(55.6, 53, 57.7, 61.7, 59.6, 50.9, 64.3, 49.5, 63.5)
y <- c(53.1, 48.8, 55.6, 60.5, 57.4, 53.5, 63.3, 47.6, 63.7)
t.test(x, y, paired = TRUE, alternative = "greater")##
## Paired t-test
##
## data: x and y
## t = 2.1468, df = 8, p-value = 0.03205
## alternative hypothesis: true mean difference is greater than 0
## 95 percent confidence interval:
## 0.1828518 Inf
## sample estimates:
## mean difference
## 1.366667Die Differenzen (x - y) werden automatisch intern
gebildet. Natürlich kann man die Differenzen auch “manuell” ermitteln
und dann einen gewöhnlichen t-Test durchführen:
##
## One Sample t-test
##
## data: d
## t = 2.1468, df = 8, p-value = 0.03205
## alternative hypothesis: true mean is greater than 0
## 95 percent confidence interval:
## 0.1828518 Inf
## sample estimates:
## mean of x
## 1.366667Dies führt natürlich zum gleichen Resultat.
8.4 Zwei-Stichproben-Tests
Auch den Zwei-Stichproben-t-Test für unabhängige Stichproben können
wir mit der Funktion t.test durchführen. Für das
“klassische” Beispiel mit gleicher Varianz benötigen wir das Argument
var.equal = TRUE. Falls wir dies weglassen, wird ein
Welch-Test durchgeführt.
x <- c(393.3, 402.9, 378.9, 381.3, 420.8, 387.9, 423.1, 412.2, 401.8, 386.9)
y <- c(365.5, 420.2, 374.8, 375.5, 356.2, 387.1, 386.3, 380.7)
mean(x); sd(x) ## zur Kontrolle mit Buch## [1] 398.91## [1] 15.89084## [1] 380.7875## [1] 18.99492##
## Two Sample t-test
##
## data: x and y
## t = 2.2062, df = 16, p-value = 0.04234
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.708753 35.536247
## sample estimates:
## mean of x mean of y
## 398.9100 380.7875Wir sehen den Wert der Teststatistik (t = 2.2062), den
p-Wert (p-value = 0.04234) sowie das
95%-Vertrauensintervall für den Unterschied der Erwartungswerte \(\mu_X - \mu_Y\)
(0.708753 35.536247).
9 Lineare Regression
9.2 Einfache lineare Regression
Wir betrachten zuerst das Beispiel mit den zwei Prüfungen:
exams <- read.table("http://stat.ethz.ch/~meier/teaching/book-intro/data/midterm.txt",
sep = ",", header = TRUE)
str(exams)## 'data.frame': 75 obs. of 2 variables:
## $ zwischenpr: num 69.8 74.2 68.5 74.5 60.2 ...
## $ schlusspr : num 62 70.2 65.2 66.8 54.2 ...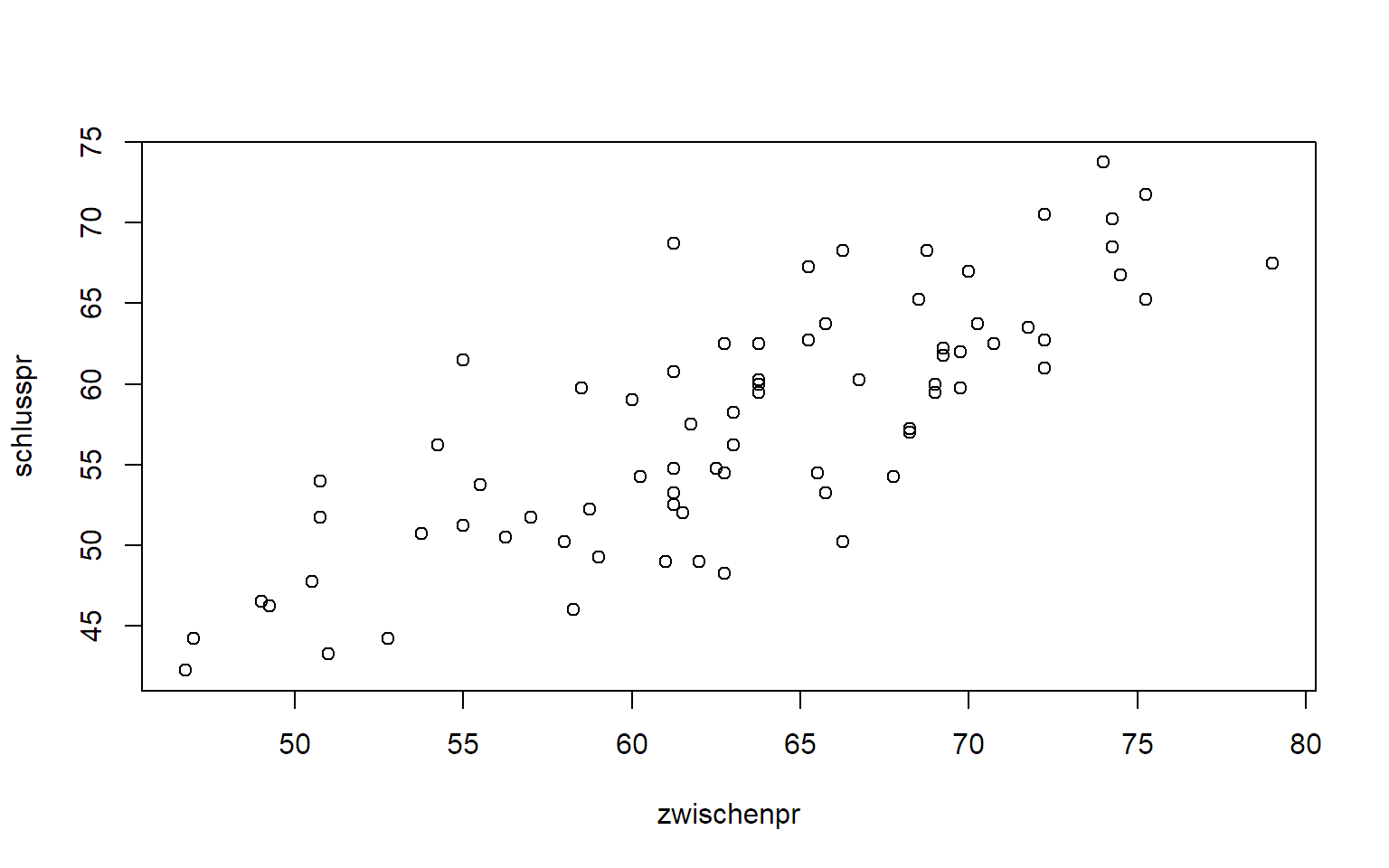
Das lineare Regressionsmodell können wir in R mit der
Funktion lm (linear model) an die Daten anpassen. Die
Modellformel lautet jeweils y ~ x (d.h., statt einem
Gleichheitszeichen verwenden wir eine Tilde um das Modell zu
spezifizieren). Die Funktion summary liefert die
geschätzten Koeffizienten inkl. der statistischen Inferenz.
##
## Call:
## lm(formula = schlusspr ~ zwischenpr, data = exams)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.8117 -2.7909 -0.4305 3.6417 12.6834
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.12633 4.54006 1.57 0.121
## zwischenpr 0.79902 0.07131 11.20 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.614 on 73 degrees of freedom
## Multiple R-squared: 0.6323, Adjusted R-squared: 0.6273
## F-statistic: 125.5 on 1 and 73 DF, p-value: < 2.2e-16In der Spalte Estimate lesen wir ab: \(\widehat{\beta}_0 = 7.13\)
((Intercept)) und \(\widehat{\beta}_1 = 0.80\)
(zwischenpr). Die entsprechenden p-Werte findet man in der
Spalte Pr(>|t|). Ferner ist \(\widehat{\sigma} = 4.61\)
(Residual standard error).
Wenn wir nur an den Koeffizienten der Modellgeraden interessiert
sind, können wir auch die Funktion coef verwenden.
## (Intercept) zwischenpr
## 7.1263321 0.7990246Entsprechende 95%-Vertrauensintervalle erhalten wir mit der Funktion
confint.
## 2.5 % 97.5 %
## (Intercept) -1.9219949 16.1746592
## zwischenpr 0.6568967 0.9411526Ein 95%-Vertrauensintervall für den Wert der Modellgeraden an der
Stelle \(x = 70\) können wir mit der
Funktion predict und dem Argument
interval = "confidence" ermitteln:
## fit lwr upr
## 1 63.05806 61.62446 64.49165Unter lwr und upr lesen wir die untere bzw.
die obere Intervallgrenze ab und erhalten so \([61.6, 64.5]\) als 95%-Vertrauensintervall
für den Wert der Geraden an der Stelle 70, d.h. für \(\beta_0 + \beta_1 \cdot 70\).
Ein 95%-Vorhersageintervall erhalten wir fast gleich, wir müssen
einfach das Argument interval = "prediction" setzen.
## fit lwr upr
## 1 63.05806 53.75105 72.36507Dies liefert das 95%-Vorhersageintervall \([53.8, 72.4]\), welches breiter als obiges Vertrauensintervall ist.
Den Tukey-Anscombe-Plot und den Normalplot der Residuen erhalten wir,
indem wir die Funktion plot auf das Modell anwenden.
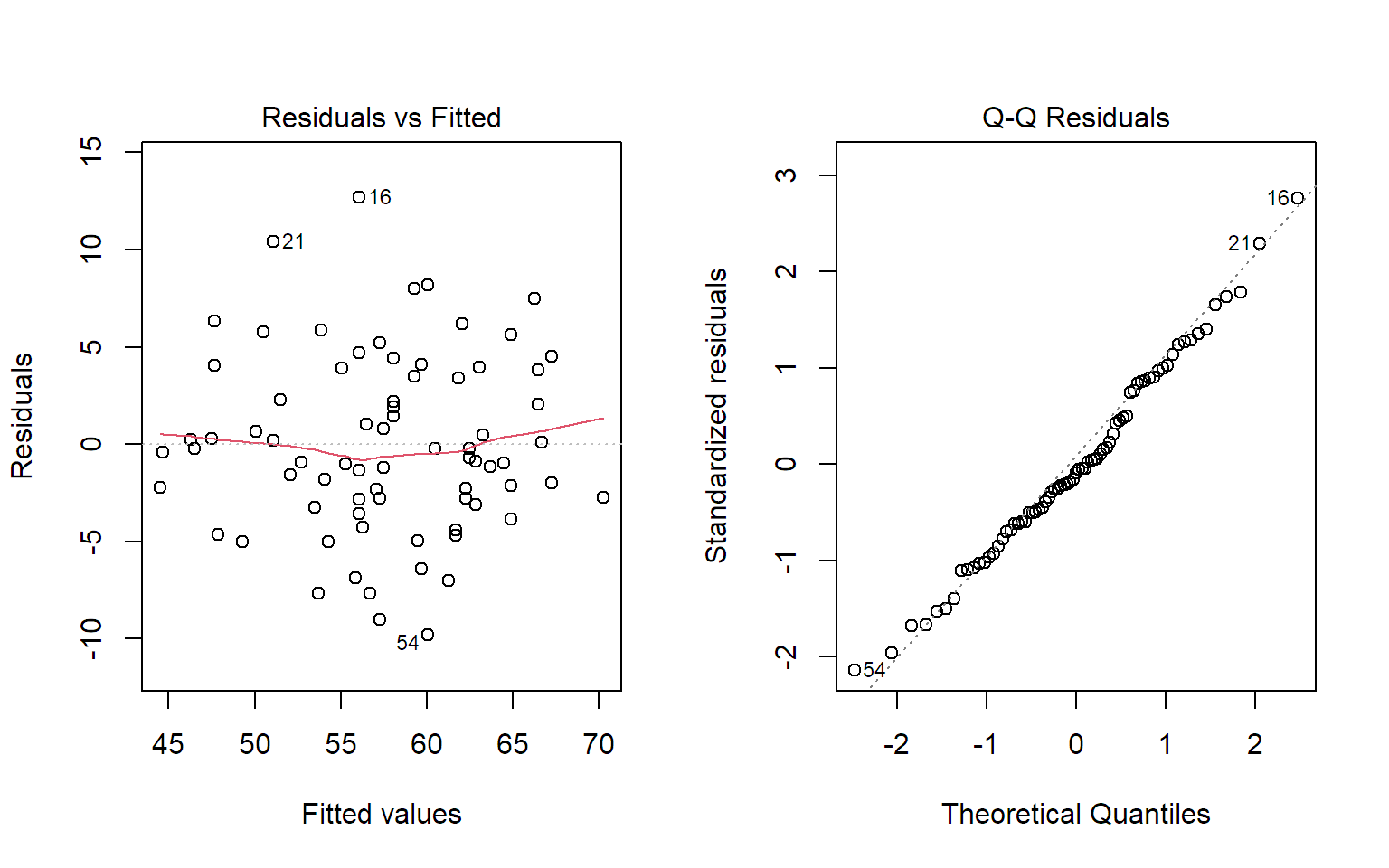
Als Ergänzung können wir auch noch die Daten mit den Telefonen und Büchern betrachten:
data.pb <- read.table("http://stat.ethz.ch/~meier/teaching/book-intro/data/phones_books.txt",
sep = ",", header = TRUE)
str(data.pb)## 'data.frame': 10 obs. of 3 variables:
## $ year : int 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017
## $ phones: int 8390 8135 7584 6603 5678 4827 4412 4037 3553 2960
## $ books : num 100 98.5 95.7 88.7 87.7 89.2 84.8 80 76.6 74.4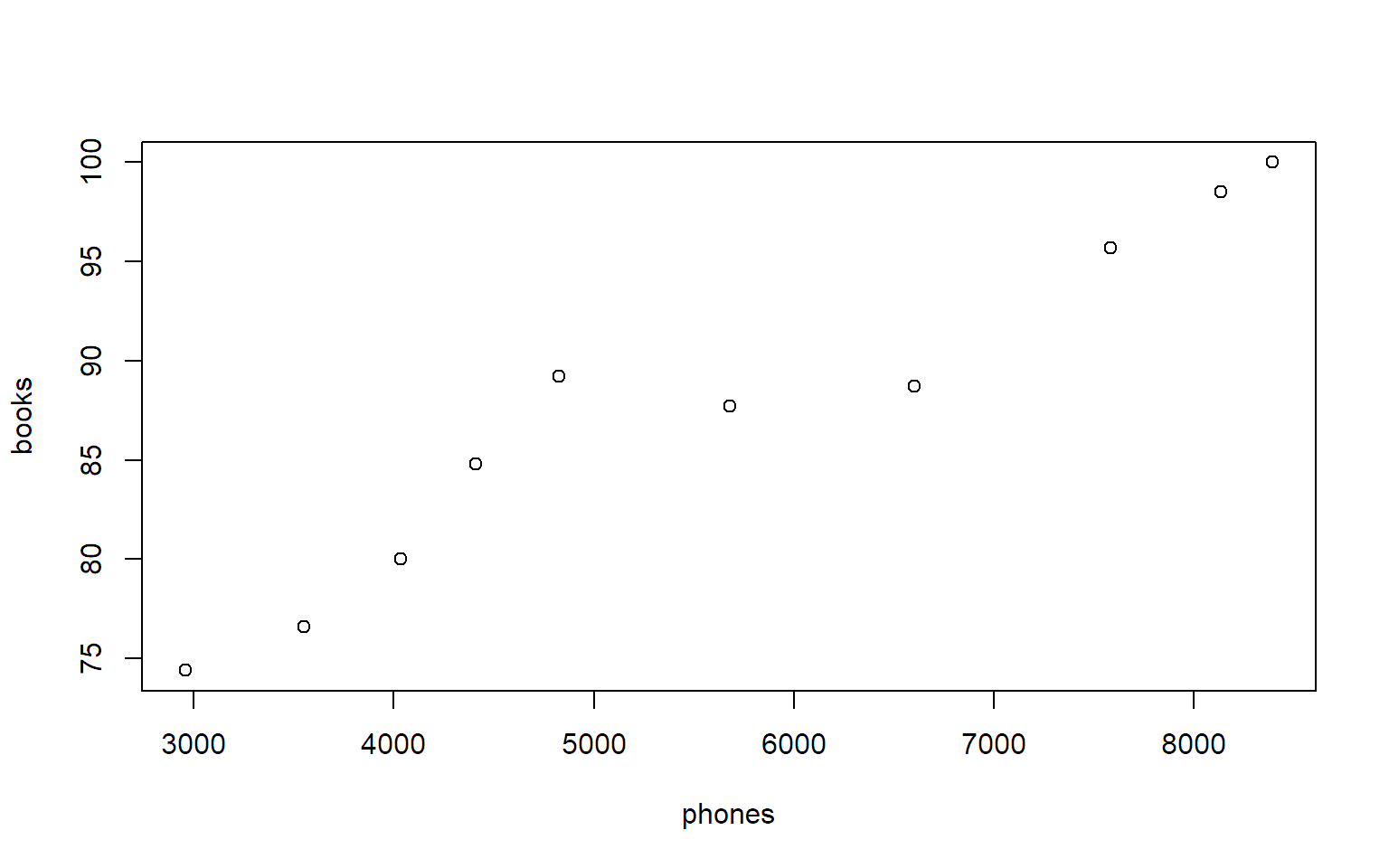
##
## Call:
## lm(formula = books ~ phones, data = data.pb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.1314 -1.4029 -0.2528 0.3216 5.0693
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.320e+01 2.488e+00 25.40 6.18e-09 ***
## phones 4.336e-03 4.203e-04 10.32 6.73e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.478 on 8 degrees of freedom
## Multiple R-squared: 0.9301, Adjusted R-squared: 0.9213
## F-statistic: 106.4 on 1 and 8 DF, p-value: 6.725e-069.3 Multiple lineare Regression
Bei der multiplen linearen Regression geht alles genau gleich. Wir
verwenden bei der Funktion lm rechts vom Zeichen
~ alle erklärenden Variablen und verbinden diese mit einem
+. Für das Beispiel aus dem Buch sieht das folgendermaßen
aus.
data <- read.table("http://stat.ethz.ch/~meier/teaching/book-intro/data/mult_reg.txt",
sep = ",", header = TRUE)
str(data)## 'data.frame': 100 obs. of 3 variables:
## $ x1: num 99.1 97.1 95.9 98.7 100.3 ...
## $ x2: num 51.2 47.1 47.1 48.4 50.7 ...
## $ y : num 37.6 52.7 55.6 47.7 46.1 ...##
## Call:
## lm(formula = y ~ x1 + x2, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.8557 -1.6011 0.0224 2.1026 5.5750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.8316 20.2374 2.314 0.022772 *
## x1 1.1651 0.3375 3.452 0.000826 ***
## x2 -2.2684 0.3310 -6.854 6.65e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.04 on 97 degrees of freedom
## Multiple R-squared: 0.4654, Adjusted R-squared: 0.4543
## F-statistic: 42.22 on 2 and 97 DF, p-value: 6.466e-14Den p-Wert des F-Tests sehen wir in der letzten Zeile
(F-statistic). Es ist p-value: 6.466e-14 und
daher wird der Globaltest deutlich verworfen. Vertrauensintervalle
erhalten wir wieder mit der Funktion confint.
## 2.5 % 97.5 %
## (Intercept) 6.665889 86.997233
## x1 0.495263 1.835026
## x2 -2.925303 -1.611564Was passiert mit dem Zusammenhang bei den Telefonen und Büchern, wenn wir die Zeit auch noch ins Modell nehmen?
data.pb <- read.table("http://stat.ethz.ch/~meier/teaching/book-intro/data/phones_books.txt",
sep = ",", header = TRUE)
str(data.pb)## 'data.frame': 10 obs. of 3 variables:
## $ year : int 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017
## $ phones: int 8390 8135 7584 6603 5678 4827 4412 4037 3553 2960
## $ books : num 100 98.5 95.7 88.7 87.7 89.2 84.8 80 76.6 74.4##
## Call:
## lm(formula = books ~ phones + year, data = data.pb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.1187 -0.6457 -0.1103 1.3166 2.2525
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.117e+03 3.042e+03 2.669 0.0321 *
## phones -1.745e-03 2.318e-03 -0.753 0.4762
## year -3.985e+00 1.505e+00 -2.648 0.0330 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.873 on 7 degrees of freedom
## Multiple R-squared: 0.9651, Adjusted R-squared: 0.9551
## F-statistic: 96.69 on 2 and 7 DF, p-value: 7.967e-06Wenn wir die Zeit auch im Modell haben, ist der Einfluss der Telefone nicht mehr gesichert.