| Type: | Package |
| Title: | Uniform Sampling |
| Version: | 0.5.0 |
| Date: | 2023-07-18 |
| Author: | Stéphane Laurent |
| Maintainer: | Stéphane Laurent <laurent_step@outlook.fr> |
| Description: | Uniform sampling on various geometric shapes, such as spheres, ellipsoids, simplices. |
| License: | GPL-3 |
| URL: | https://github.com/stla/uniformly |
| BugReports: | https://github.com/stla/uniformly/issues |
| Imports: | abind, pgnorm, rgl, stats |
| Suggests: | geometry, knitr, misc3d, rmarkdown, scatterplot3d |
| VignetteBuilder: | knitr |
| Encoding: | UTF-8 |
| RoxygenNote: | 7.2.3 |
| NeedsCompilation: | no |
| Packaged: | 2023-07-18 07:15:32 UTC; SDL96354 |
| Repository: | CRAN |
| Date/Publication: | 2023-07-18 17:40:02 UTC |
Make hexahedron
Description
Make a hexahedron for usage in
runif_in_hexahedron and other functions.
Usage
makeHexahedron(p0, p1, p2, p3, p4, p5, p6, p7)
Arguments
p0, p1, p2, p3, p4, p5, p6, p7 |
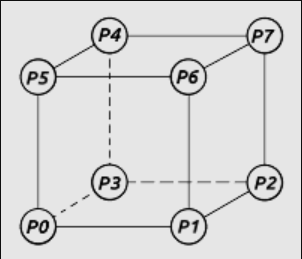
the eight vertices of the hexahedron, as in the figure shown below |
Details
A hexahedron is a polyhedron having six quad faces. Its eight vertices must be placed as in the figure below.
Value
A matrix with eight columns, the vertices.
See Also
The function plotHexahedron is useful to check the
hexahedron.
Examples
library(uniformly)
# a non-convex hexahedron
hexahedron <- makeHexahedron(
p0 = c(1.5, 1.5, 0),
p1 = c(2, 0, 0),
p2 = c(2, 2, 0),
p3 = c(0, 2, 0),
p4 = c(0, 2, 2),
p5 = c(0, 0, 2),
p6 = c(2, 0, 2),
p7 = c(2, 2, 2)
)
plotHexahedron(hexahedron)
Plot hexahedron
Description
Plot a hexahedron with rgl.
Usage
plotHexahedron(hexahedron, alpha = 1)
Arguments
hexahedron |
a hexahedron given by a 3 times 8 matrix; see
|
alpha |
opacity, a number between 0 and 1 |
Value
No returned value, called for plotting.
Examples
library(uniformly)
hexahedron <- makeHexahedron(
p0 = c(0, 0, 0),
p1 = c(2, 0, 0),
p2 = c(2, 2, 0),
p3 = c(0, 2, 0),
p4 = c(0.5, 1.5, 2),
p5 = c(0.5, 0.5, 2),
p6 = c(1.5, 0.5, 2),
p7 = c(1.5, 1.5, 2)
)
plotHexahedron(hexahedron)
Sampling on hemisphere
Description
Sampling on a hemisphere according to the Phong density (dimension 3).
Usage
rphong_on_hemisphere(n, alpha = 0, r = 1)
Arguments
n |
number of simulations |
alpha |
parameter of the Phong density, a positive number;
|
r |
radius |
Value
The simulations in a n times 3 matrix.
Examples
## Not run:
library(rgl)
sims <- rphong_on_hemisphere(400, alpha = 10)
spheres3d(0, 0, 0, color = "red", alpha = 0.5)
points3d(sims)
## End(Not run)
Uniform sampling on/in cube
Description
Uniform sampling on or in a cube (arbitrary dimension).
Usage
runif_in_cube(n, d, O = rep(0, d), r = 1)
runif_on_cube(n, d, O = rep(0, d), r = 1)
Arguments
n |
number of simulations |
d |
dimension |
O |
center of the cube |
r |
radius (half-side) of the cube |
Value
The simulations in a n times d matrix.
Examples
sims <- runif_on_cube(60, d = 2)
plot(sims, xlim = c(-1,1), ylim = c(-1,1), pch = 19, asp = 1)
sims <- runif_in_cube(50, d = 3)
library(scatterplot3d)
scatterplot3d(sims, pch = 19, highlight.3d = TRUE, asp = 1)
Uniform sampling on/in ellipsoid
Description
Uniform sampling on an ellipsoid or in an ellipsoid. The sampling in an ellipsoid is available in arbitrary dimension. The sampling on an ellipsoid is available only in dimension 2 or 3.
Usage
runif_on_ellipse(n, A, r)
runif_on_ellipsoid(n, A, r)
runif_in_ellipsoid(n, A, r)
Arguments
n |
number of simulations |
A |
symmetric positive-definite matrix defining the ellipsoid (see
Details), of size 2 for |
r |
"radius" (see Details) |
Details
The ellipsoid is the set of vectors x satisfying
t(x) %*% A %*% x == r^2. For example, for an axis-aligned
ellipse with horizontal radius a and vertical radius b, take
A=1/diag(c(a^2,b^2)) and r=1.
Value
The simulations in a matrix with n rows.
Examples
library(uniformly)
set.seed(666L)
# ellipse parameters
A <- rbind(c(2, 1), c(1, 1))
r <- 2
# plot the ellipse
x1 <- seq(-2.5, 2.5, length.out = 100)
x2 <- seq(-3, 3, length.out = 100)
z <- outer(
x1, x2, FUN = Vectorize(function(x1, x2) t(c(x1, x2)) %*% A %*% c(x1, x2))
)
contour(x1, x2, z, nlevels = 1, levels = r^2, asp = 1, drawlabels = FALSE)
# simulations on the perimeter
sims <- runif_on_ellipse(60, A, r)
points(sims, pch = 19, col = "blue")
# simulations in the area
sims <- runif_in_ellipsoid(100, A, r)
points(sims, pch = 19, col = "green")
# 3D example ####
A <- matrix(c(5,1,1, 1,3,1, 1,1,1), ncol = 3L)
r <- 2
# draw the ellipsoid
library(misc3d)
x <- seq(-1, 1, length.out = 50)
y <- seq(-1.5, 1.5, length.out = 50)
z <- seq(-2.7, 2.7, length.out = 50)
g <- as.matrix(expand.grid(x = x, y = y, z = z))
voxel <-
array(apply(g, 1L, function(v) t(v) %*% A %*% v), dim = c(50, 50, 50))
isosurface <- computeContour3d(voxel, max(voxel), r^2, x = x, y = y, z = z)
drawScene.rgl(makeTriangles(isosurface, alpha = 0.3))
# simulate and plot points on ellipsoid
library(rgl)
sims <- runif_on_ellipsoid(300, A, r)
points3d(sims)
Uniform sampling in an annulus
Description
Uniform sampling in an annulus (dimension 2).
Usage
runif_in_annulus(n, O, r1, r2)
Arguments
n |
number of simulations |
O |
center of the annulus |
r1 |
inner radius |
r2 |
outer radius |
Value
The simulations in a n times 2 matrix.
Examples
sims <- runif_in_annulus(100, c(0, 0), 1, 2)
plot(sims, xlim = c(-2, 2), ylim = c(-2, 2), asp = 1, pch = 19)
Uniform sampling in a hexahedron
Description
Uniform sampling in a hexahedron (polyhedron with six faces).
Usage
runif_in_hexahedron(n, hexahedron)
Arguments
n |
number of simulations |
hexahedron |
a hexahedron given by a 3 times 8 matrix whose eight
columns are the vertices; see |
Value
The simulations in a n times 3 matrix.
Examples
library(uniformly)
hexahedron <- makeHexahedron(
p0 = c(0, 0, 0),
p1 = c(2, 0, 0),
p2 = c(2, 2, 0),
p3 = c(0, 2, 0),
p4 = c(0.5, 1.5, 2),
p5 = c(0.5, 0.5, 2),
p6 = c(1.5, 0.5, 2),
p7 = c(1.5, 1.5, 2)
)
sims <- runif_in_hexahedron(200, hexahedron)
plotHexahedron(hexahedron, alpha = 0.3)
rgl::points3d(sims)
Uniform sampling in a p-ball
Description
Uniform sampling in a p-ball (arbitrary dimension).
Usage
runif_in_pball(n, d, p, r = 1)
Arguments
n |
number of simulations |
d |
dimension |
p |
exponent in the p-norm, a positive number |
r |
positive number, the radius |
Value
The simulations in a n times d matrix.
Examples
sims <- runif_in_pball(500, d = 2, p = 1)
plot(sims, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1)
Uniform sampling in a polygon
Description
Uniform sampling in a polygon (dimension 2).
Usage
runif_in_polygon(n, vertices, center = "centroid")
Arguments
n |
number of simulations |
vertices |
two-columns matrix giving the vertices (rows); the vertices must be ordered (clockwise or counterclockwise) |
center |
a point with respect to which the polygon is star-shaped, or
|
Details
This function works for a star-shaped polygon, that is, a polygon
that contains a point from which the entire polygon boundary is visible.
This point must be given in the center argument. If the polygon is
convex, any point inside the polygon is suitable (thus the default option
of the center argument is appropriate in this case).
Value
The simulations in a n times 2 matrix.
Examples
vs <- matrix(c(0.951056516295154, 0.309016994374947,
0.224513988289793, 0.309016994374947,
-0.951056516295154, 0.309016994374948,
-0.363271264002681, -0.118033988749895,
0.587785252292473, -0.809016994374948,
0.36327126400268, -0.118033988749895,
0, 1,
-0.224513988289793, 0.309016994374947,
-0.587785252292473, -0.809016994374947,
0, -0.381966011250105),
ncol=2, byrow=TRUE)
sims <- runif_in_polygon(500, vs)
plot(sims, xlim = c(-1, 1), ylim = c(-1, 1), pch = 19, asp = 1)
Uniform sampling in a simplex
Description
Uniform sampling in a simplex (arbitrary dimension).
Usage
runif_in_simplex(n, simplex)
Arguments
n |
number of simulations |
simplex |
a |
Value
The simulations in a n times d matrix.
Note
In dimension 3, you can use runif_in_tetrahedron instead.
Examples
simplex <- rbind(c(0,0,0), c(1,0,0), c(1,1,0), c(1,1,2))
sims <- runif_in_simplex(1000, simplex)
library(rgl)
points3d(sims)
Uniform sampling in a tetrahedron
Description
Uniform sampling in a tetrahedron (in dimension 3).
Usage
runif_in_tetrahedron(n, v1, v2, v3, v4)
Arguments
n |
number of simulations |
v1, v2, v3, v4 |
vertices of the tetrahedron |
Value
The simulations in a n times 3 matrix.
See Also
runif_in_simplex for sampling in a simplex in
arbitrary dimension.
Examples
library(rgl)
tetrahedron <- tetrahedron3d()
shade3d(tetrahedron, color = "red", alpha = 0.3)
vs <- tetrahedron$vb[1L:3L, ]
sims <- runif_in_tetrahedron(100, vs[, 1], vs[, 2], vs[, 3], vs[, 4])
points3d(sims)
Uniform sampling on a spherical patch
Description
Uniform sampling on a spherical patch (in dimension 3).
Usage
runif_on_spherePatch(n, r = 1, phi1, phi2, theta1, theta2)
Arguments
n |
number of simulations |
r |
radius |
phi1, phi2 |
numbers defining the latitudinal angle range |
theta1, theta2 |
numbers defining the longitudinal angle range |
Details
A sphere patch is the part of the sphere whose polar angles
theta and phi satisfy
0 <= theta1 <= theta <= theta2 <= 2*pi and
0 <= phi1 <= phi <= phi2 <= pi.
Value
The simulations in a n times 3 matrix.
See Also
runif_on_stri for sampling on a spherical triangle.
Examples
# sampling on the first orthant:
sims <-
runif_on_spherePatch(100, phi1 = 0, phi2 = pi/2, theta1 = 0, theta2 = pi/2)
## Not run:
library(rgl)
spheres3d(0, 0, 0, color = "red", alpha = 0.5)
points3d(sims)
## End(Not run)
Uniform sampling on a spherical cap
Description
Uniform sampling on a spherical cap (in dimension 3).
Usage
runif_on_sphericalCap(n, r = 1, h)
Arguments
n |
number of simulations |
r |
radius of the sphere |
h |
height of the cap |
Value
The simulations in a n times 3 matrix.
Examples
sims <- runif_on_sphericalCap(500, r = 2, h = 1)
## Not run:
library(rgl)
spheres3d(0, 0, 0, radius = 2, color = "red", alpha = 0.5)
points3d(sims)
## End(Not run)
Uniform sampling on a spherical triangle
Description
Uniform sampling on a spherical triangle (in dimension 3).
Usage
runif_on_stri(n, r = 1, v1, v2, v3)
Arguments
n |
number of simulations |
r |
radius |
v1, v2, v3 |
vertices |
Value
The simulations in a n times 3 matrix.
Examples
# sampling on the first orthant:
sims <- runif_on_stri(100, v1 = c(1, 0, 0), v2 = c(0, 1, 0), v3 = c(0, 0, 1))
## Not run:
library(rgl)
spheres3d(0, 0, 0, color = "red", alpha = 0.5)
points3d(sims)
## End(Not run)
Uniform sampling on/in sphere
Description
Uniform sampling on a sphere or in a sphere, in arbitrary dimension.
Usage
runif_on_sphere(n, d, r = 1)
runif_in_sphere(n, d, r = 1)
Arguments
n |
number of simulations |
d |
dimension of the space |
r |
radius of the sphere |
Value
The simulations in a n times d matrix.
Examples
sims <- runif_on_sphere(20, d = 2)
plot(sims, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1, pch = 19)
sims <- runif_in_sphere(100, d = 2)
plot(sims, xlim = c(-1, 1), ylim = c(-1, 1), asp = 1, pch = 19)
Uniform sampling on/in torus
Description
Uniform sampling on or in a torus (dimension 3).
Usage
runif_on_torus(n, R, r)
runif_in_torus(n, R, r)
Arguments
n |
number of simulations |
R |
major radius |
r |
minor radius |
Value
The simulations in a n times 3 matrix.
Examples
R <- 3; r <- 2
sims_on <- runif_on_torus(50, R = R, r = r)
sims_in <- runif_in_torus(50, R = R, r = r)
library(misc3d)
fx <- function(u,v) (R+r*cos(u)) * cos(v)
fy <- function(u,v) (R+r*cos(u)) * sin(v)
fz <- function(u,v) r*sin(u)
parametric3d(
fx, fy, fz, umin = 0, umax = 2*pi, vmin = 0, vmax = 2*pi, alpha = 0.3
)
library(rgl)
points3d(sims_on)
points3d(sims_in, color = "red")
Uniform sampling on/in a triangle
Description
Uniform sampling on or in a triangle (dimension 2).
Usage
runif_in_triangle(n, v1, v2, v3)
runif_on_triangle(n, v1, v2, v3)
Arguments
n |
number of simulations |
v1, v2, v3 |
vertices of the triangle |
Value
The simulations in a n times 2 matrix.
Examples
sims <- runif_on_triangle(30, c(0,0), c(1,0), c(0,1))
plot(sims, xlim = c(0,1), ylim = c(0,1), pch = 19)
sims <- runif_in_triangle(100, c(0,0), c(1,0), c(0,1))
plot(sims, xlim = c(0,1), ylim = c(0,1), pch = 19)
Uniform sampling on/in a unit simplex
Description
Uniform sampling on or in a unit simplex (arbitrary dimension).
Usage
runif_on_unitSimplex(n, d)
runif_in_unitSimplex(n, d)
Arguments
n |
number of simulations |
d |
dimension of the space |
Value
The simulations in a n times d matrix.
See Also
runif_in_tetrahedron for sampling in an arbitrary
tetrahedron in dimension 3; runif_in_simplex for sampling
in an arbitrary simplex.
Examples
library(rgl)
sims <- runif_on_unitSimplex(300, d = 3)
points3d(sims)
Sphere surface
Description
Surface of a sphere (arbitrary dimension).
Usage
surface_sphere(d, r = 1)
Arguments
d |
dimension of the space |
r |
radius of the sphere |
Value
The surface of the sphere of radius r in the
d-dimensional space.
Examples
r <- 2
surface_sphere(3, r)
4*pi*r^2
# perimeter of the unit circle:
surface_sphere(2)
Sphere patch surface
Description
Surface of a sphere patch.
Usage
surface_spherePatch(r, phi1, phi2, theta1, theta2)
Arguments
r |
radius |
phi1, phi2 |
numbers defining the latitudinal angle range |
theta1, theta2 |
numbers defining the longitudinal angle range |
Details
A sphere patch is the part of the sphere whose polar angles
theta and phi satisfy
0 <= theta1 <= theta <= theta2 <= 2*pi and
0 <= phi1 <= phi <= phi2 <= pi.
Value
The surface of the sphere patch.
See Also
surface_stri for the surface of a spherical triangle.
Examples
# surface of the first orthant:
surface_spherePatch(r=1, phi1=0, phi2=pi/2, theta1=0, theta2=pi/2)
surface_stri(r=1, c(1,0,0), c(0,1,0), c(0,0,1))
Spherical cap surface
Description
Surface of a spherical cap.
Usage
surface_sphericalCap(r, h)
Arguments
r |
radius of the sphere |
h |
height of the cap |
Value
The surface area of the spherical cap.
Spherical triangle surface
Description
Surface of a spherical triangle.
Usage
surface_stri(r, v1, v2, v3)
Arguments
r |
radius |
v1, v2, v3 |
vertices |
Value
The surface of the spherical triangle of radius r with
vertices v1, v2, v3.
Examples
# surface of the first orthant:
surface_stri(r=1, c(1,0,0), c(0,1,0), c(0,0,1))
Torus surface
Description
Surface of a torus.
Usage
surface_torus(R, r)
Arguments
R |
major radius |
r |
minor radius |
Value
The surface area of the torus.
Triangle surface
Description
Surface of a triangle.
Usage
surface_triangle(v1, v2, v3)
Arguments
v1, v2, v3 |
vertices of the triangle |
Value
The surface of the triangle with vertices v1, v2,
v3.
Examples
surface_triangle(c(0,0), c(0,1), c(1,0))
Ellipsoid volume
Description
Volume of an ellipsoid (arbitrary dimension).
Usage
volume_ellipsoid(A, r)
Arguments
A |
symmetric positive-definite matrix defining the ellipsoid (see Details) |
r |
"radius" (see Details) |
Details
The (boundary of the) ellipsoid is the set of vectors x
satisfying t(x) %*% A %*% x == r^2.
Value
The volume of the ellipsoid.
Examples
# dimension 2 (area), with diagonal matrix A
A <- diag(c(2,3))
r <- 2
volume_ellipsoid(A, r)
pi * r^2 / sqrt(A[1,1]*A[2,2])
Hexahedron volume
Description
Volume of a hexahedron.
Usage
volume_hexahedron(hexahedron)
Arguments
hexahedron |
a 3 times 8 matrix whose columns are the eight vertices
of the hexahedron; see |
Value
The volume of the hexahedron.
Examples
library(uniformly)
# a cube with side 2 ####
hexahedron <- makeHexahedron(
p0 = c(0, 0, 0),
p1 = c(2, 0, 0),
p2 = c(2, 2, 0),
p3 = c(0, 2, 0),
p4 = c(0, 2, 2),
p5 = c(0, 0, 2),
p6 = c(2, 0, 2),
p7 = c(2, 2, 2)
)
volume_hexahedron(hexahedron) # should be 8
p-ball volume
Description
Euclidean volume of a p-ball (arbitrary dimension).
Usage
volume_pball(d, p, r = 1)
Arguments
d |
dimension |
p |
exponent in the p-norm, a positive number |
r |
radius of the ball |
Value
The volume of the p-ball with radius r.
Examples
volume_pball(d=4, p=2, r=2)
volume_sphere(d=4, r=2)
Simplex volume
Description
Volume of a simplex (arbitrary dimension).
Usage
volume_simplex(simplex)
Arguments
simplex |
a |
Value
The volume of the simplex.
Examples
set.seed(666)
simplex <- matrix(rnorm(4*3), nrow=4, ncol=3)
volume_simplex(simplex)
volume_tetrahedron(simplex[1,], simplex[2,], simplex[3,], simplex[4,])
Sphere volume
Description
Volume of a sphere (arbitrary dimension).
Usage
volume_sphere(d, r = 1)
Arguments
d |
dimension of the space |
r |
radius of the sphere |
Value
The volume of the sphere with radius r in the
d-dimensional space.
Examples
r <- 2
volume_sphere(3, r)
4/3*pi*r^3
Spherical cap volume
Description
Volume of a spherical cap.
Usage
volume_sphericalCap(r, h)
Arguments
r |
radius of the sphere |
h |
height of the cap |
Value
The volume of the spherical cap.
Tetrahedron volume
Description
Volume of a tetrahedron (dimension 3).
Usage
volume_tetrahedron(v1, v2, v3, v4)
Arguments
v1, v2, v3, v4 |
vertices of the tetrahedron |
Value
The volume of the tetrahedron.
See Also
volume_simplex for the volume of a simplex in
arbitrary dimension.
Examples
v1 <- c(0,0,0); v2 <- c(1,0,0); v3 <- c(0,1,0); v4 <- c(0,0,1)
volume_tetrahedron(v1, v2, v3, v4)
volume_unitSimplex(3)
Torus volume
Description
Volume of a torus.
Usage
volume_torus(R, r)
Arguments
R |
major radius |
r |
minor radius |
Value
The volume of the torus.
Unit simplex volume
Description
Volume of the unit simplex (arbitrary dimension).
Usage
volume_unitSimplex(d)
Arguments
d |
dimension of the space |
Value
The volume of the unit simplex in the space of dimension d.
See Also
volume_simplex for the volume of an arbitrary simplex.