The rEDM package is a collection of methods for
Empirical Dynamic Modeling (EDM). EDM is based on the mathematical
theory of reconstructing attractor manifolds from time series data, with
applications to forecasting, causal inference, and more. It is based on
research software developed for the Sugihara Lab (University of
California San Diego, Scripps Institution of Oceanography).
This package implements an R wrapper of EDM tools from the cppEDM library. Introduction and documentation are are avilable online, or in the package tutorial.
Functionality includes:
To install from CRAN rEDM:
install.packages(rEDM)Using R devtools for latest development version:
install.packages("devtools")
devtools::install_github("SugiharaLab/rEDM")Building from source:
git clone https://github.com/SugiharaLab/rEDM.git
cd rEDM
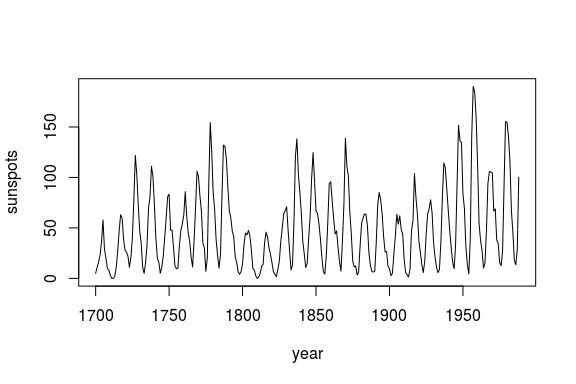
R CMD INSTALL .We begin by looking at annual time series of sunspots:
df = data.frame(yr = as.numeric(time(sunspot.year)),
sunspot_count = as.numeric(sunspot.year))
plot(df$yr, df$sunspot_count, type = "l",
xlab = "year", ylab = "sunspots")
First, we use EmbedDimension() to determine the optimal
embedding dimension, E:
library(rEDM) # load the package
# If you're new to the rEDM package, please consult the tutorial:
# vignette("rEDM-tutorial")
E.opt = EmbedDimension( dataFrame = df, # input data
lib = "1 280", # portion of data to train
pred = "1 280", # portion of data to predict
columns = "sunspot_count",
target = "sunspot_count" )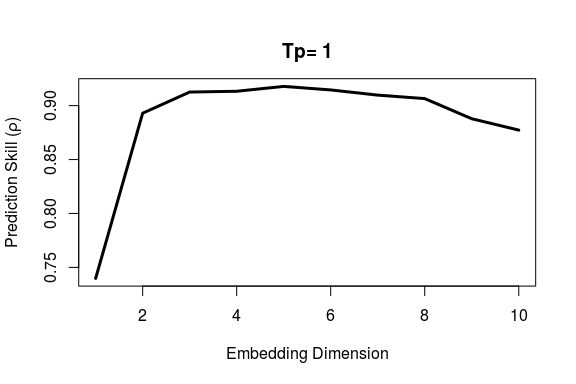
E.opt
# E rho
# 1 1 0.7397
# 2 2 0.8930
# 3 3 0.9126
# 4 4 0.9133
# 5 5 0.9179
# 6 6 0.9146
# 7 7 0.9098
# 8 8 0.9065
# 9 9 0.8878
# 10 10 0.8773Highest predictive skill is found between E = 3 and
E = 6. Since we generally want a simpler model, if
possible, we use E = 3 to forecast the last 1/3 of data
based on training (attractor reconstruction) from the first 2/3.
simplex = Simplex( dataFrame = df,
lib = "1 190", # portion of data to train
pred = "191 287", # portion of data to predict
columns = "sunspot_count",
target = "sunspot_count",
E = 3 )
plot( df$yr, df$sunspot_count, type = "l", lwd = 2,
xlab = "year", ylab = "sunspots")
lines( simplex$yr, simplex$Predictions, col = "red", lwd = 2)
legend( 'topleft', legend = c( "Observed", "Predicted (year + 1)" ),
fill = c( 'black', 'red' ), bty = 'n', cex = 1.3 )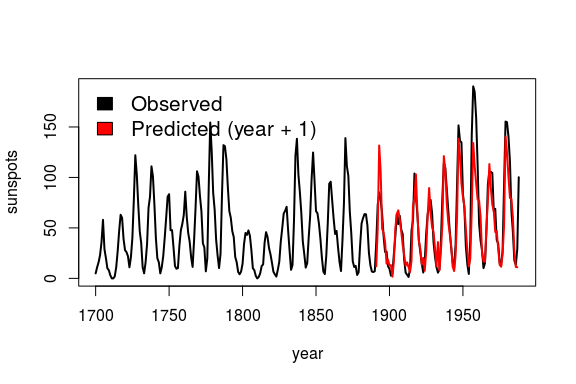
Please see the package vignettes for more details:
browseVignettes("rEDM")Sugihara G. and May R. 1990. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature, 344:734–741.
Sugihara G. 1994. Nonlinear forecasting for the classification of natural time series. Philosophical Transactions: Physical Sciences and Engineering, 348 (1688) : 477–495.
Dixon, P. A., M. Milicich, and G. Sugihara, 1999. Episodic fluctuations in larval supply. Science 283:1528–1530.
Sugihara G., May R., Ye H., Hsieh C., Deyle E., Fogarty M., Munch S., 2012. Detecting Causality in Complex Ecosystems. Science 338:496-500.
Ye H., and G. Sugihara, 2016. Information leverage in interconnected ecosystems: Overcoming the curse of dimensionality. Science 353:922–925.