
Sometimes magic is just someone spending more time on something than anyone else might reasonably expect. – Teller
Generate mazes recursively via Turtle graphics.
– Steven E. Pav, shabbychef@gmail.com
This package can be installed from CRAN, via drat, or from github:
# via CRAN:
install.packages("mazealls")
# via drat:
if (require(drat)) {
drat:::add("shabbychef")
install.packages("mazealls")
}
# get snapshot from github (may be buggy)
if (require(devtools)) {
install_github("shabbychef/mazealls")
}The simplest maze to generate recursively is a parallelogram. One can
generate a parallelogram maze by splitting the domain into two parts by
an arbitrary cut line with a hole in it, and then recursively creating
mazes on both parts. Unlike some shapes, this method applies for
arbitrary (integral) side lengths, where by ‘length’ we mean in units of
‘hallway widths’, what we call the unit_len in the API.
Here is a simple parallelogram maze:
library(TurtleGraphics)
library(mazealls)
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 400)
turtle_right(90)
parallelogram_maze(angle = 90, unit_len = 10, width = 75,
height = 55, method = "uniform", draw_boundary = TRUE)
})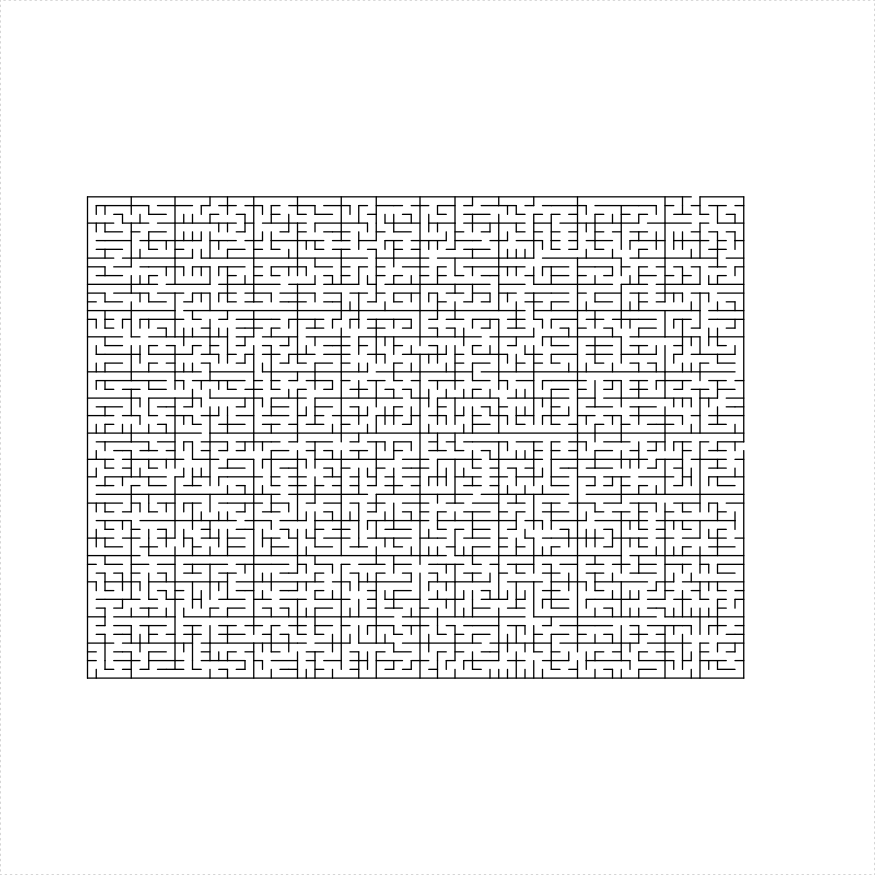
plot of chunk para-maze
The parallelogram_maze function admits a
balance parameter which controls how the maze should be
recursively subdivided. A negative value creates imbalanced mazes, while
positive values create more uniform mazes. In the example below we
create seven mazes side by side with an increasing balance
parameter:
library(TurtleGraphics)
library(mazealls)
turtle_init(2000, 2000)
turtle_hide()
turtle_up()
turtle_do({
turtle_left(90)
turtle_forward(930)
turtle_right(90)
valseq <- seq(from = -1.5, to = 1.5, length.out = 7)
blines <- c(1, 2, 3, 4)
bholes <- c(1, 3)
set.seed(1234)
for (iii in seq_along(valseq)) {
parallelogram_maze(angle = 90, unit_len = 12,
width = 22, height = 130, method = "two_parallelograms",
draw_boundary = TRUE, balance = valseq[iii],
end_side = 3, boundary_lines = blines,
boundary_holes = bholes)
turtle_right(180)
blines <- c(2, 3, 4)
bholes <- c(3)
}
})
plot of chunk para-imbalance-fade
The parallelogram_maze can be drawn in a Hilbert
Curve:
library(TurtleGraphics)
library(mazealls)
turtle_init(1020, 1020, mode = "clip")
turtle_hide()
turtle_up()
turtle_do({
turtle_setpos(15, 15)
turtle_setangle(0)
parallelogram_maze(angle = 90, unit_len = 10, width = 96,
height = 96, method = "hilbert", hilbert_balance = 4,
height_boustro = c(30, 2), width_boustro = c(30,
2), boundary_holes = c(1, 4), start_from = "corner",
boundary_hole_locations = c(1, 1, 1, 1), draw_boundary = TRUE)
})
plot of chunk para-hilbert
An equilateral triangle maze can be constructed in a number of different ways:
I illustrate them here:
library(TurtleGraphics)
library(mazealls)
# uniform method
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = 6, unit_len = 12, method = "uniform",
draw_boundary = TRUE)
})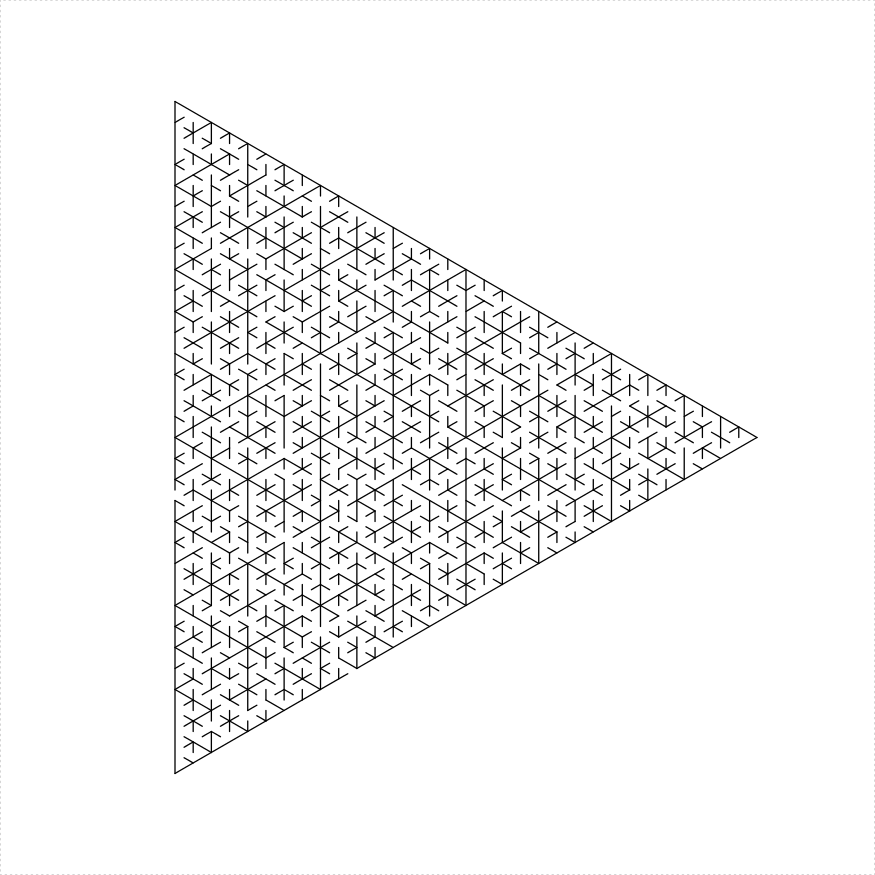
plot of chunk eq-tri-uniform
library(TurtleGraphics)
library(mazealls)
# stacked trapezoids
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = 6, unit_len = 12, method = "stack_trapezoids",
draw_boundary = TRUE)
})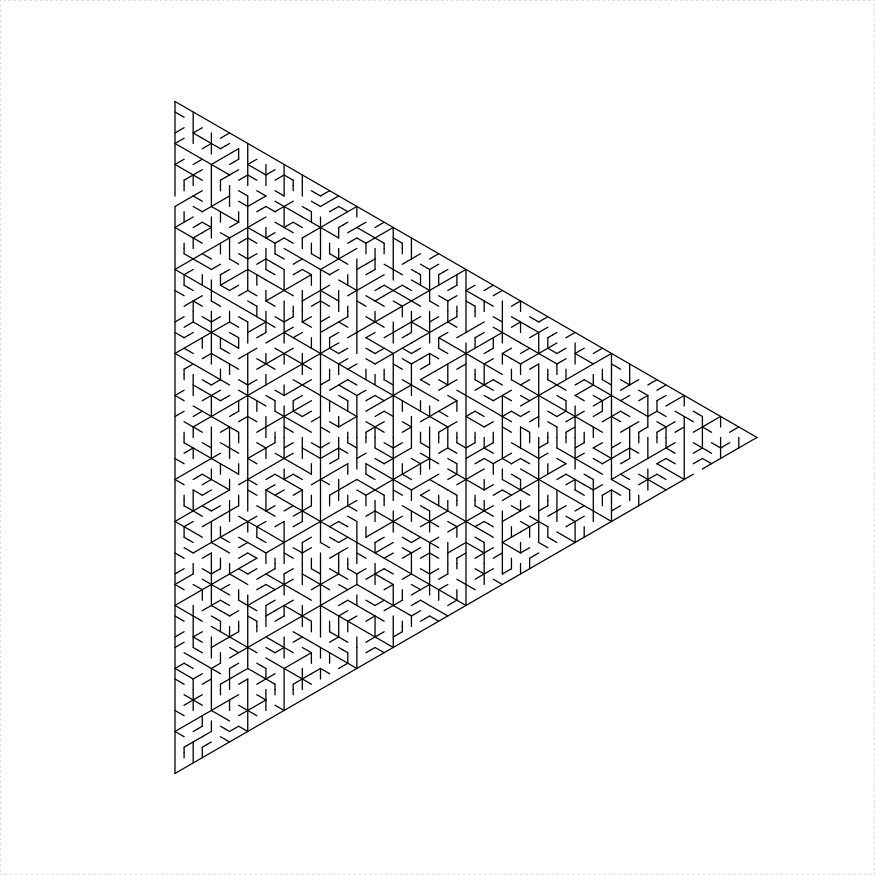
plot of chunk eq-tri-stack
library(TurtleGraphics)
library(mazealls)
# four triangles
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = 6, unit_len = 12, method = "triangles",
draw_boundary = TRUE)
})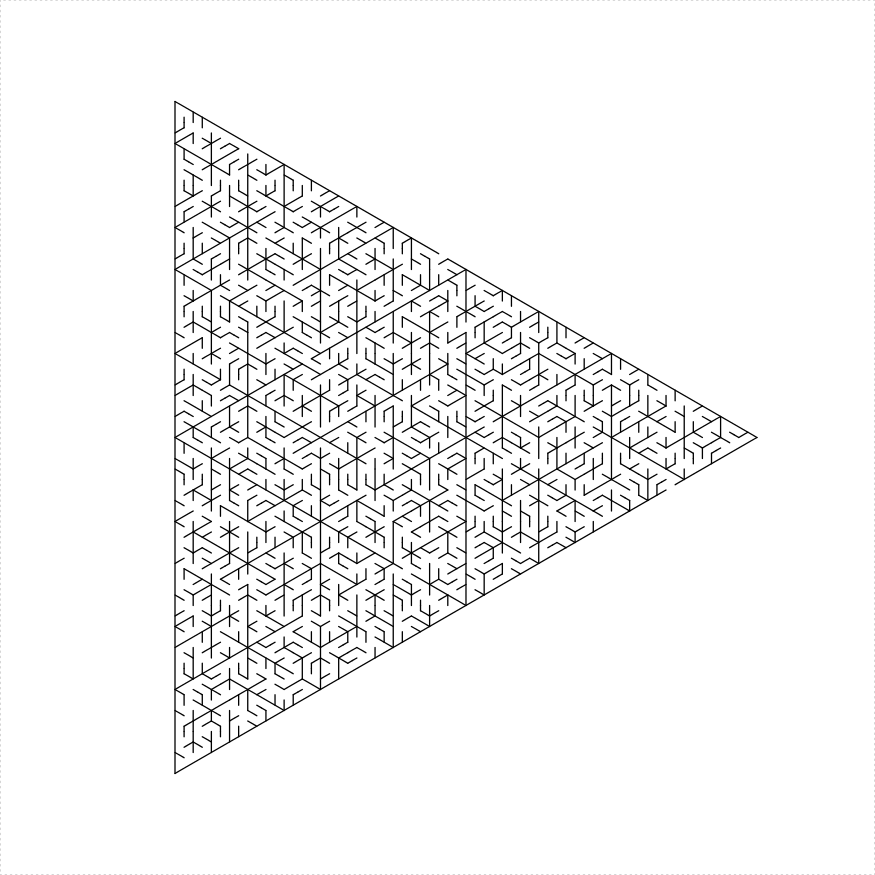
plot of chunk eq-tri-four-tri
library(TurtleGraphics)
library(mazealls)
# two ears
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = 6, unit_len = 12, method = "two_ears",
draw_boundary = TRUE)
})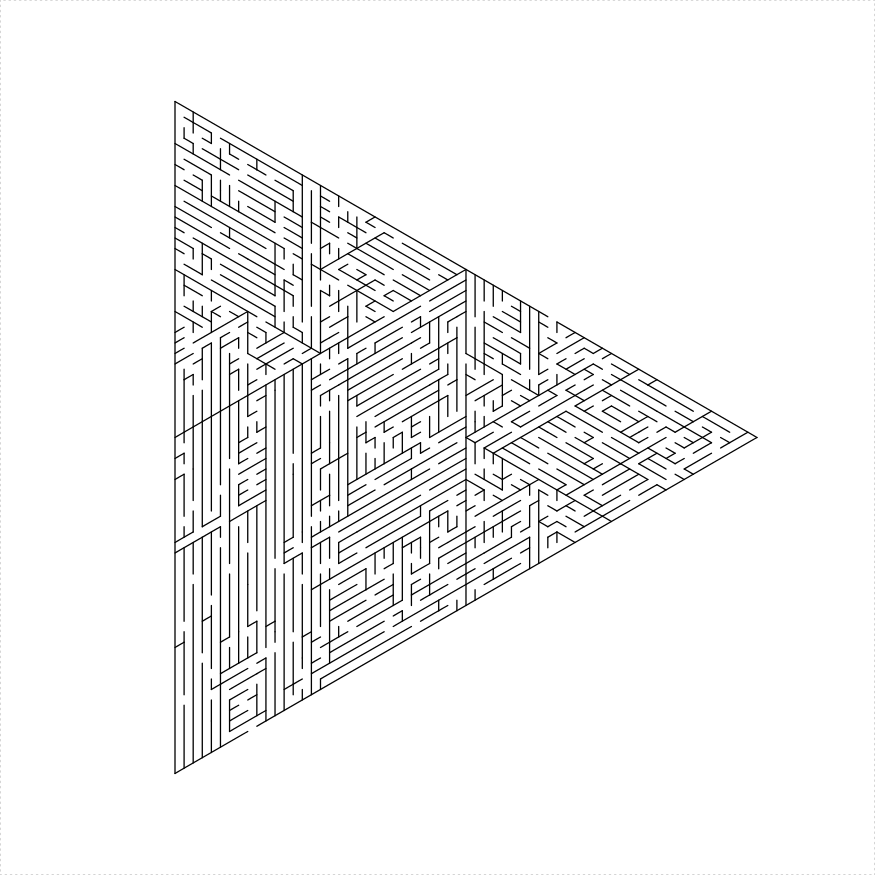
plot of chunk eq-tri-two-ears
library(TurtleGraphics)
library(mazealls)
# hex and three
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = log2(66), unit_len = 12,
method = "hex_and_three", draw_boundary = TRUE)
})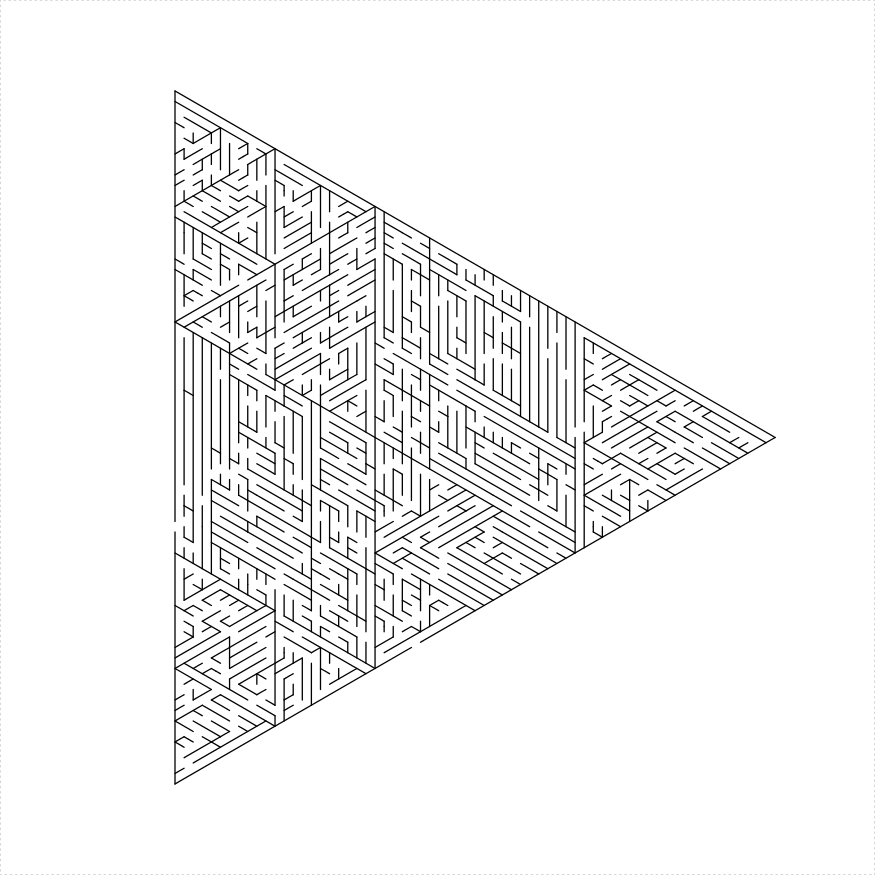
plot of chunk eq-tri-hex-and-three
library(TurtleGraphics)
library(mazealls)
# shave
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = log2(66), unit_len = 12,
method = "shave", draw_boundary = TRUE)
})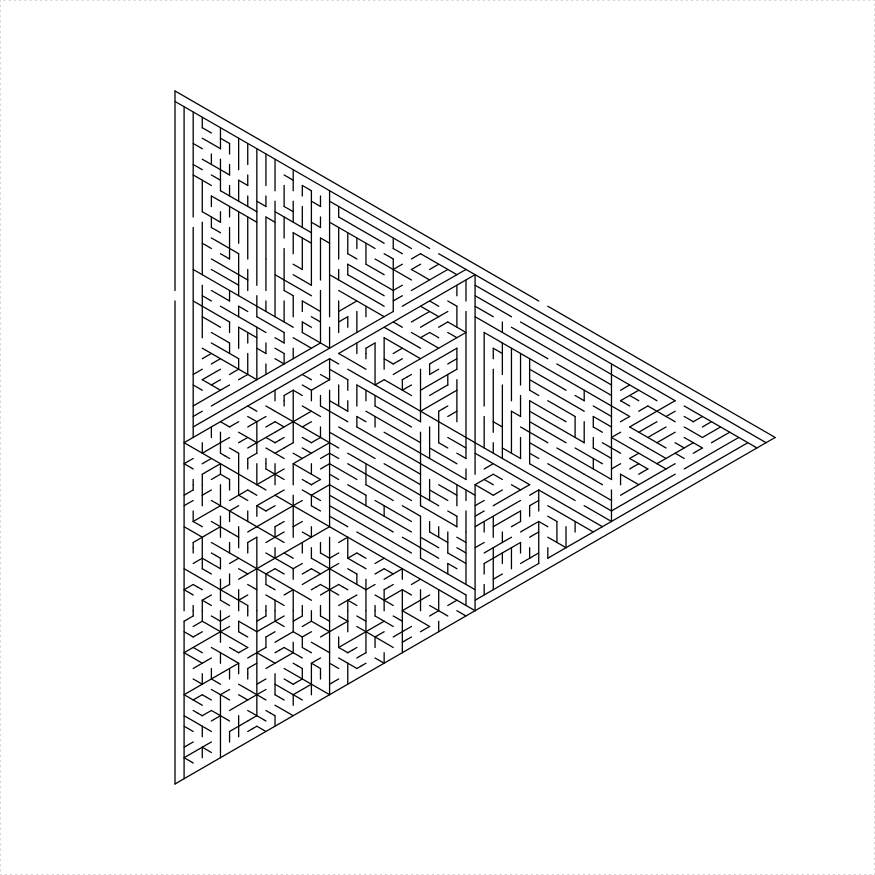
plot of chunk eq-tri-shave
library(TurtleGraphics)
library(mazealls)
# shave all
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
eq_triangle_maze(depth = log2(66), unit_len = 12,
method = "shave_all", draw_boundary = TRUE,
boustro = c(35, 2))
})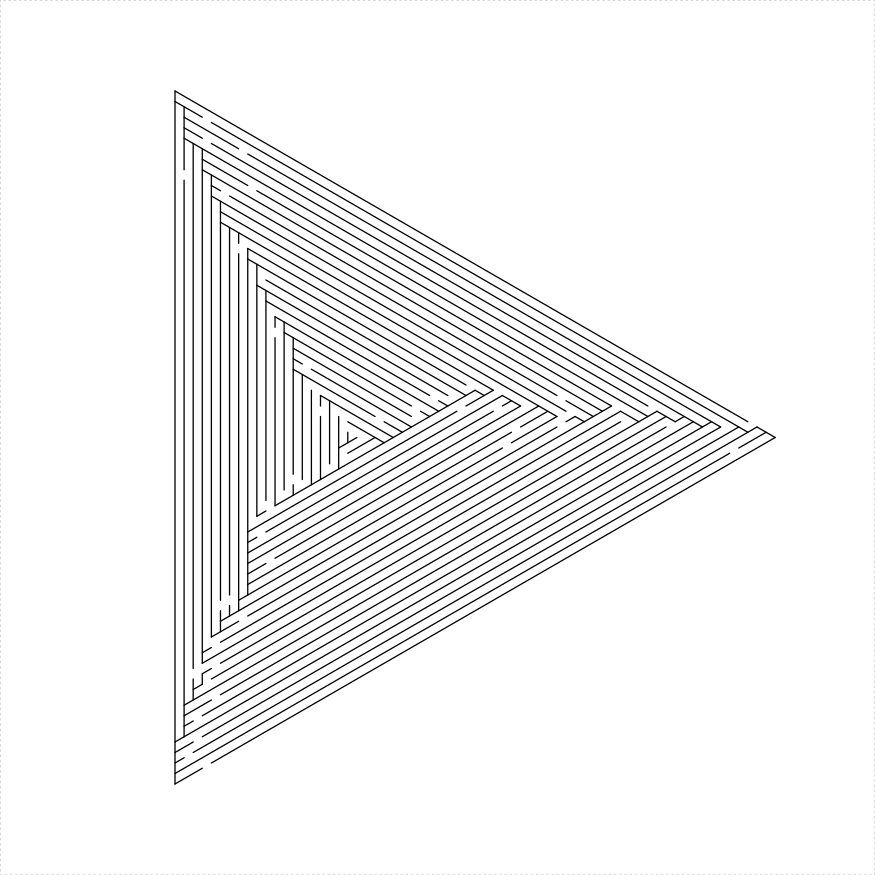
plot of chunk eq-tri-shave-all
An regular hexagonal maze can be constructed in a number of different ways:
library(TurtleGraphics)
library(mazealls)
# two trapezoids
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
hexagon_maze(depth = 5, unit_len = 12, method = "two_trapezoids",
draw_boundary = TRUE)
})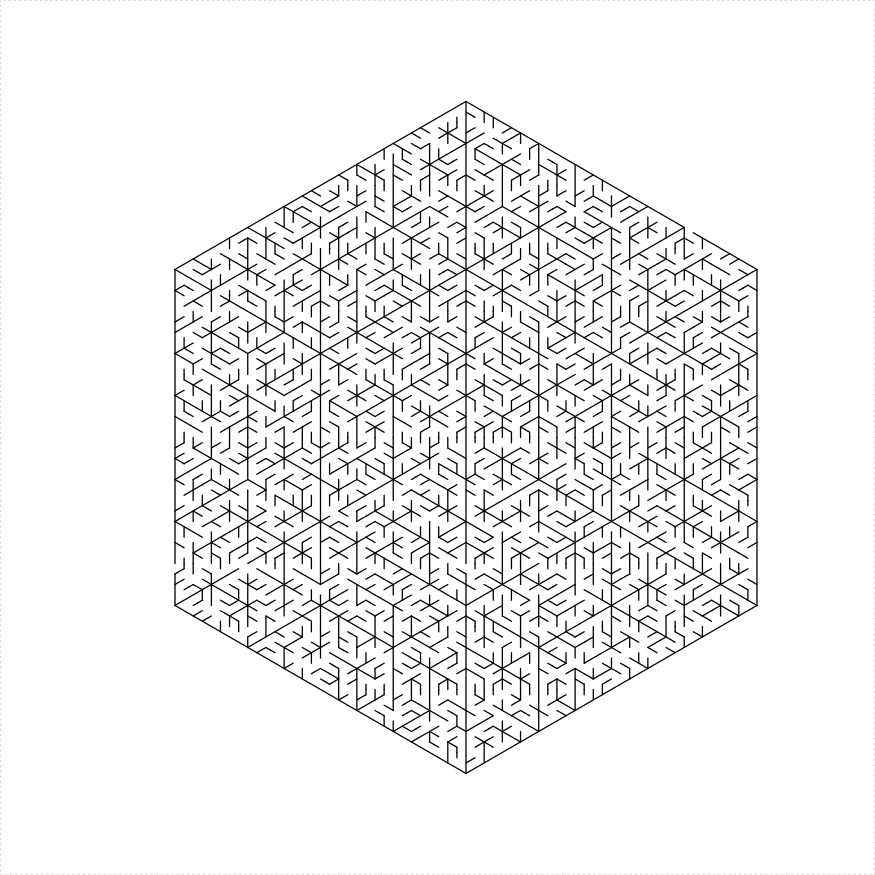
plot of chunk hex-trapezoids
library(TurtleGraphics)
library(mazealls)
# six triangles
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
hexagon_maze(depth = 5, unit_len = 12, method = "six_triangles",
draw_boundary = TRUE, boundary_hole_arrows = TRUE)
})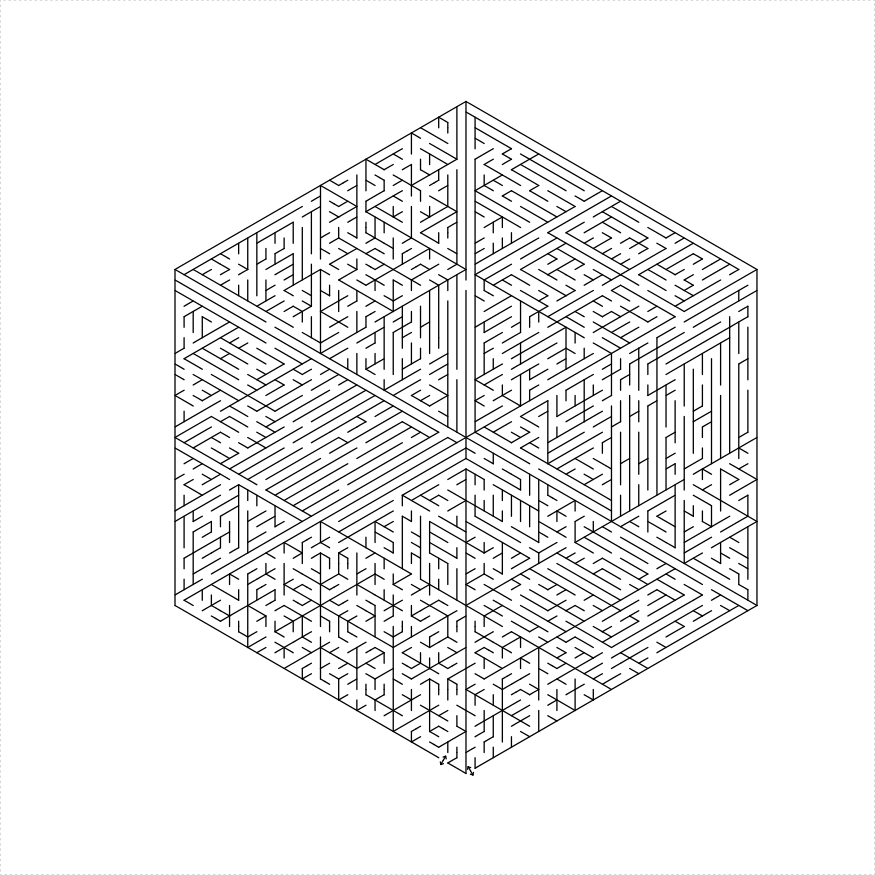
plot of chunk hex-triangles
library(TurtleGraphics)
library(mazealls)
# six triangles
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
hexagon_maze(depth = 5, unit_len = 12, method = "three_parallelograms",
draw_boundary = TRUE, boundary_hole_arrows = TRUE)
})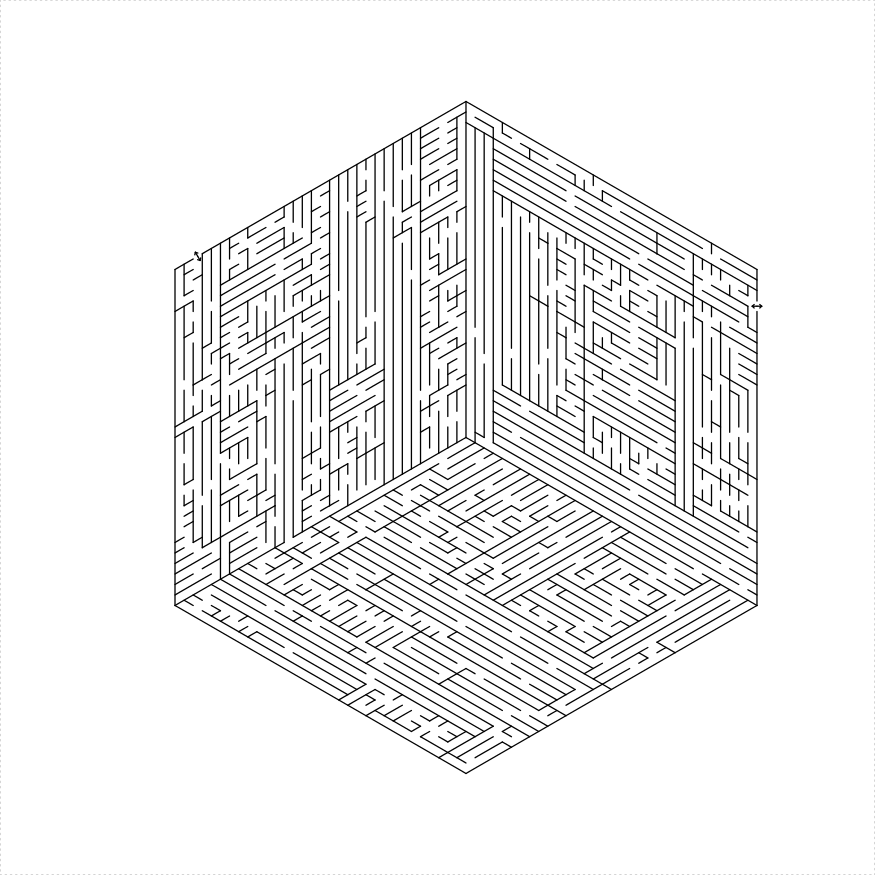
plot of chunk hex-parallelo
A dodecagon can be dissected into a hexagon and a ring of alternating squares and equilateral triangles:
library(TurtleGraphics)
library(mazealls)
# dodecagon
turtle_init(2200, 2200, mode = "clip")
turtle_hide()
turtle_up()
turtle_do({
turtle_setpos(80, 1100)
turtle_setangle(0)
dodecagon_maze(depth = log2(27), unit_len = 20,
draw_boundary = TRUE, boundary_holes = c(1,
7))
})
plot of chunk simple-dodecagon
An isosceles trapezoid maze can be constructed in a number of different ways:
library(TurtleGraphics)
library(mazealls)
# four trapezoids
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
iso_trapezoid_maze(depth = 5, unit_len = 12, method = "four_trapezoids",
draw_boundary = TRUE)
})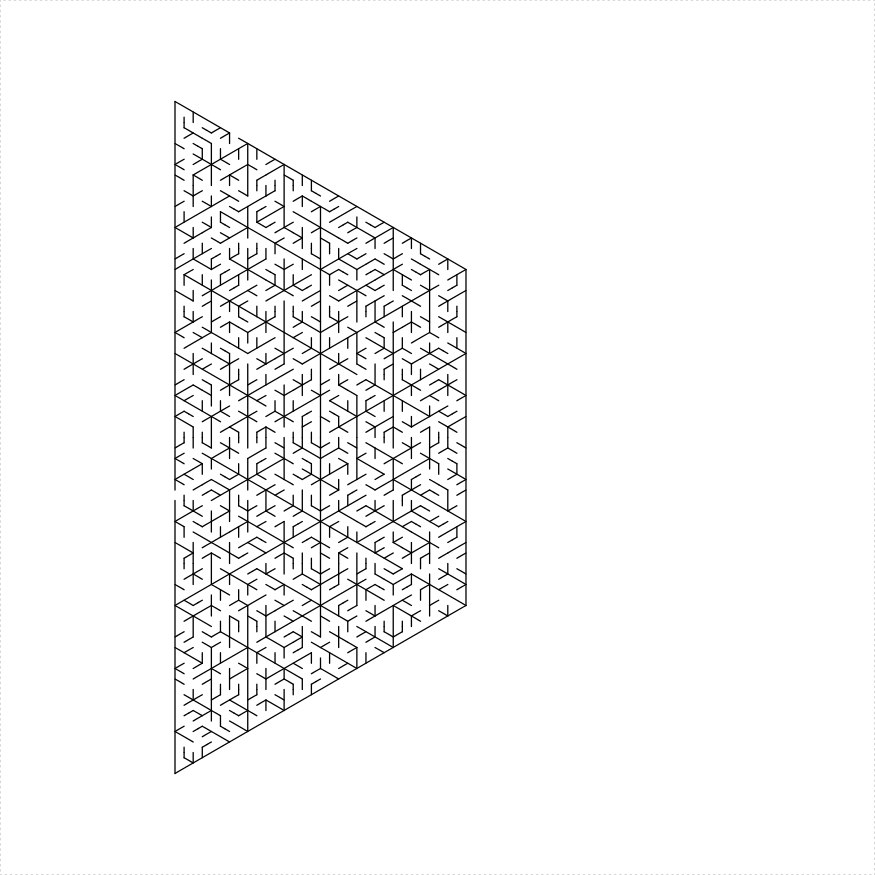
plot of chunk trap-four
library(TurtleGraphics)
library(mazealls)
# one ear
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 300)
turtle_right(90)
iso_trapezoid_maze(depth = 5, unit_len = 12, method = "one_ear",
draw_boundary = TRUE)
})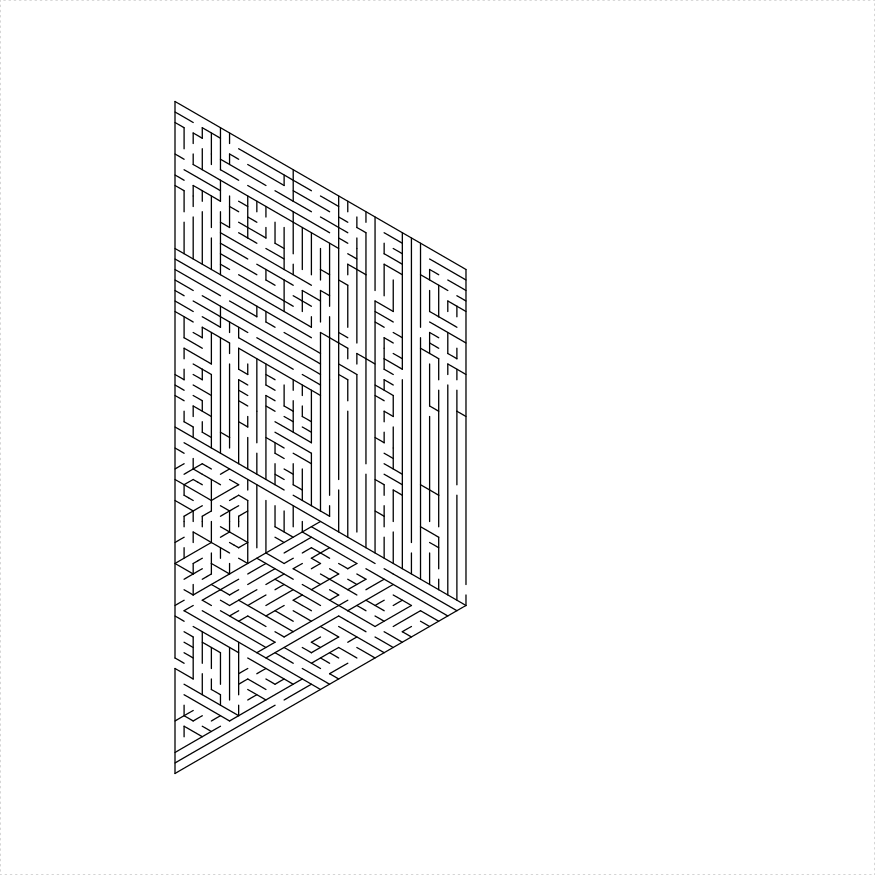
plot of chunk trap-ear
Regular 2n gons usually admit a dissection into rhombuses. Sometimes, however, these have extremely acute angles, which do not translate into nice mazes. At the moment, there is only support for octagons, and decagons. While a dodecagon would also admit such a dissection, this would require extremely acute angles which would make an ugly maze.
library(TurtleGraphics)
library(mazealls)
# octagon
turtle_init(2000, 2000, mode = "clip")
turtle_hide()
turtle_up()
turtle_do({
turtle_setpos(75, 1000)
turtle_setangle(0)
octagon_maze(log2(48), 16, draw_boundary = TRUE,
boundary_holes = c(1, 5))
})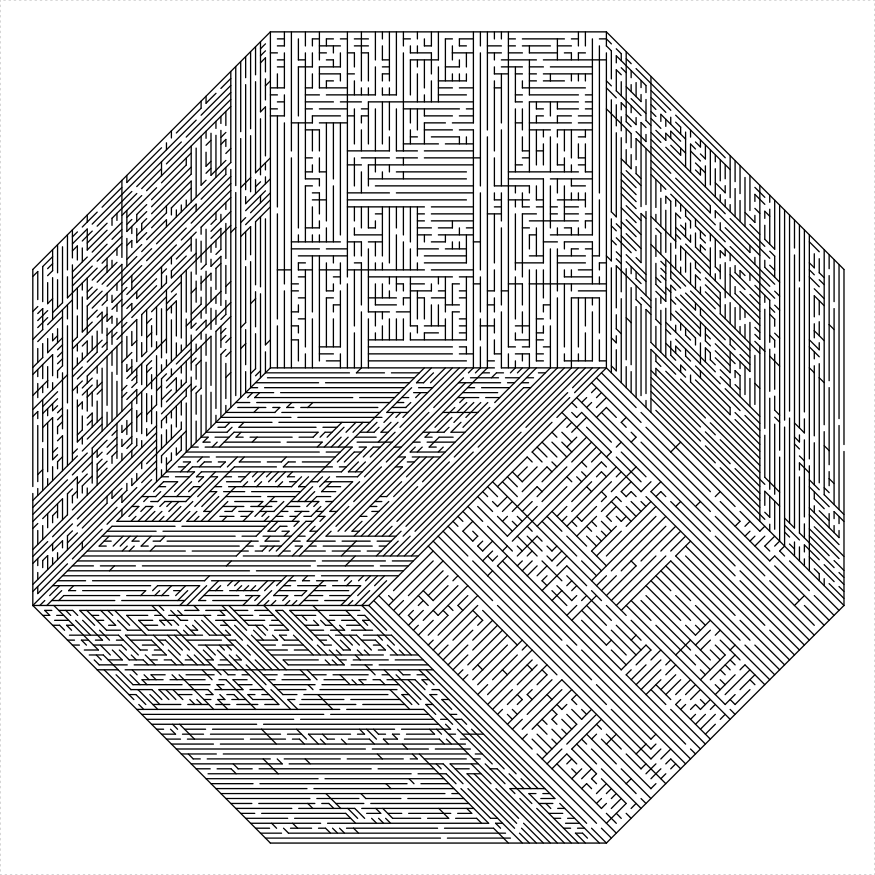
plot of chunk simple-octagon
library(TurtleGraphics)
library(mazealls)
# decagon
turtle_init(2200, 2200, mode = "clip")
turtle_hide()
turtle_up()
turtle_do({
turtle_setpos(60, 1100)
turtle_setangle(0)
decagon_maze(5, 21, draw_boundary = TRUE, boundary_holes = c(1,
6))
})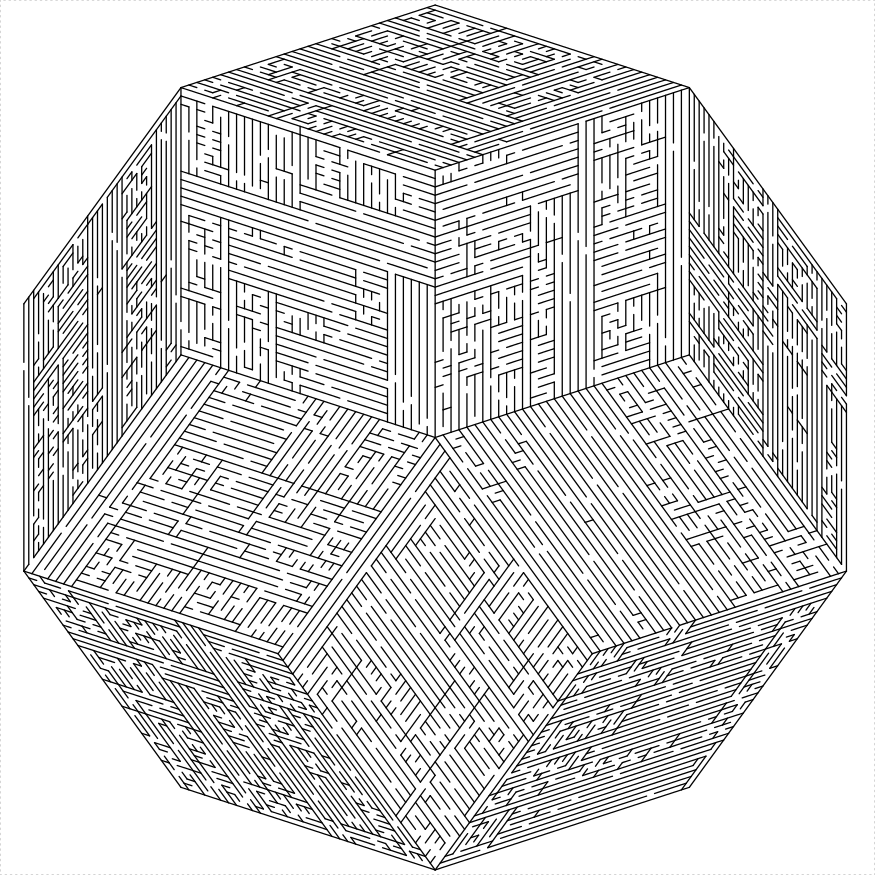
plot of chunk simple-decagon
Everyone’s favorite snowflake can also be a maze. Simply fill in triangle bumps with triangular mazes and create lines with holes as needed:
library(TurtleGraphics)
library(mazealls)
# koch flake
turtle_init(1000, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 200)
turtle_right(90)
turtle_backward(distance = 300)
koch_maze(depth = 4, unit_len = 8)
})
plot of chunk koch-flake
Koch flakes of different sizes tile the plane:
library(TurtleGraphics)
library(mazealls)
# koch flake
turtle_init(2000, 2000, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(450, 1000)
turtle_setangle(60)
ul <- 12
dep <- 4
koch_maze(depth = dep, unit_len = ul, clockwise = TRUE,
draw_boundary = FALSE)
turtle_left(30)
turtle_col("gray40")
dropdown <- 1
for (iii in c(1:6)) {
if (iii == 1) {
bholes <- c(1, 2)
} else if (iii == 4) {
bholes <- c(1, 3)
} else {
bholes <- c(1)
}
koch_maze(depth = dep - dropdown, unit_len = ul *
(3^(dropdown - 0.5)), clockwise = FALSE,
draw_boundary = TRUE, boundary_holes = bholes,
boundary_hole_arrows = c(2, 3))
turtle_forward(3^(dep - 1) * ul * sqrt(3))
turtle_right(60)
}
})
plot of chunk koch-meta-flake
Similarly, one can construct a maze in a Sierpinski triangle.
library(TurtleGraphics)
library(mazealls)
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(50, 1250)
turtle_setangle(0)
sierpinski_maze(unit_len = 19, depth = 7, draw_boundary = TRUE,
boundary_lines = TRUE, boundary_holes = c(1,
3), color1 = "black", color2 = "gray60")
})
plot of chunk sierpinski
And a Sierpinski Carpet:
library(TurtleGraphics)
library(mazealls)
turtle_init(800, 1000)
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(50, 450)
turtle_setangle(0)
sierpinski_carpet_maze(angle = 80, unit_len = 8,
width = 90, height = 90, draw_boundary = TRUE,
boundary_holes = c(1, 3), balance = 1.5, color2 = "green")
})
plot of chunk sierpinski-carpet
library(TurtleGraphics)
library(mazealls)
turtle_init(2000, 2000, mode = "clip")
turtle_hide()
turtle_up()
bholes <- list(c(1, 2), c(1), c(2))
turtle_do({
turtle_setpos(1000, 1000)
turtle_setangle(180)
for (iii in c(1:3)) {
mybhol <- bholes[[iii]]
sierpinski_carpet_maze(angle = 120, unit_len = 11,
width = 81, height = 81, draw_boundary = TRUE,
boundary_lines = c(1, 2, 3), num_boundary_holes = 0,
boundary_holes = mybhol, balance = 1, color2 = "green",
start_from = "corner")
turtle_left(120)
}
})
plot of chunk menger-sponge
One can make four different kinds of Sierpinski trapezoids, the traditional four triangles, a hexaflake, and something like a Dragon fractal:
library(TurtleGraphics)
library(mazealls)
turtle_init(1050, 600, mode = "clip")
turtle_hide()
turtle_up()
turtle_do({
for (iii in c(1:4)) {
turtle_setpos(40 + (iii - 1) * 250, 300)
turtle_setangle(0)
sierpinski_trapezoid_maze(unit_len = 8, depth = 5,
draw_boundary = TRUE, start_from = "midpoint",
num_boundary_holes = 2, boundary_holes = c(2,
4), color2 = "green", flip_color_parts = iii) # this controls fractal style
}
})
plot of chunk sierpinski-trapezoids
library(TurtleGraphics)
library(mazealls)
turtle_init(1250, 1100, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(50, 550)
turtle_setangle(30)
sierpinski_hexagon_maze(depth = 6, unit_len = 9,
boundary_lines = TRUE, draw_boundary = TRUE,
boundary_holes = c(1, 3), start_from = "corner",
color1 = "black", color2 = "green", style = "sierpinski")
})
plot of chunk sierpinski-hexagon
A hexaflake is a cross between a Koch snowflake and a Sierpinski triangle, at least in theory.
library(TurtleGraphics)
library(mazealls)
# hexaflake
long_side <- 2400
inner_side <- long_side * sqrt(3)/2
sidelen <- long_side/2
dep <- 4
ul <- floor(sidelen/(3^dep))
true_wid <- 2 * ul * 3^dep * sqrt(3)/2
turtle_init(ceiling(1.1 * inner_side), ceiling(1.1 *
long_side), mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(0.5 * (ceiling(1.1 * inner_side) -
true_wid), 0.55 * long_side)
turtle_setangle(0)
hexaflake_maze(depth = dep, unit_len = floor(sidelen/(3^dep)),
draw_boundary = TRUE, color2 = "gray80")
})
plot of chunk hexaflake
The unit_len parameter controls the graphical length of
one ‘unit’, which is the length of holes between sections of the mazes,
and is roughly the width of the ‘hallways’ of a maze. Here is an example
of using different unit lengths in a stack of trapezoids
library(TurtleGraphics)
library(mazealls)
# stack some trapezoids with different unit_len
turtle_init(2500, 2500)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 800)
turtle_right(90)
clockwise <- TRUE
for (iii in c(1:6)) {
iso_trapezoid_maze(depth = 5, unit_len = 2^(6 -
iii), method = "four_trapezoids", draw_boundary = TRUE,
clockwise = clockwise, end_side = 3, start_from = "midpoint",
boundary_lines = c(1, 2, 4), boundary_holes = c(1))
clockwise <- !clockwise
}
})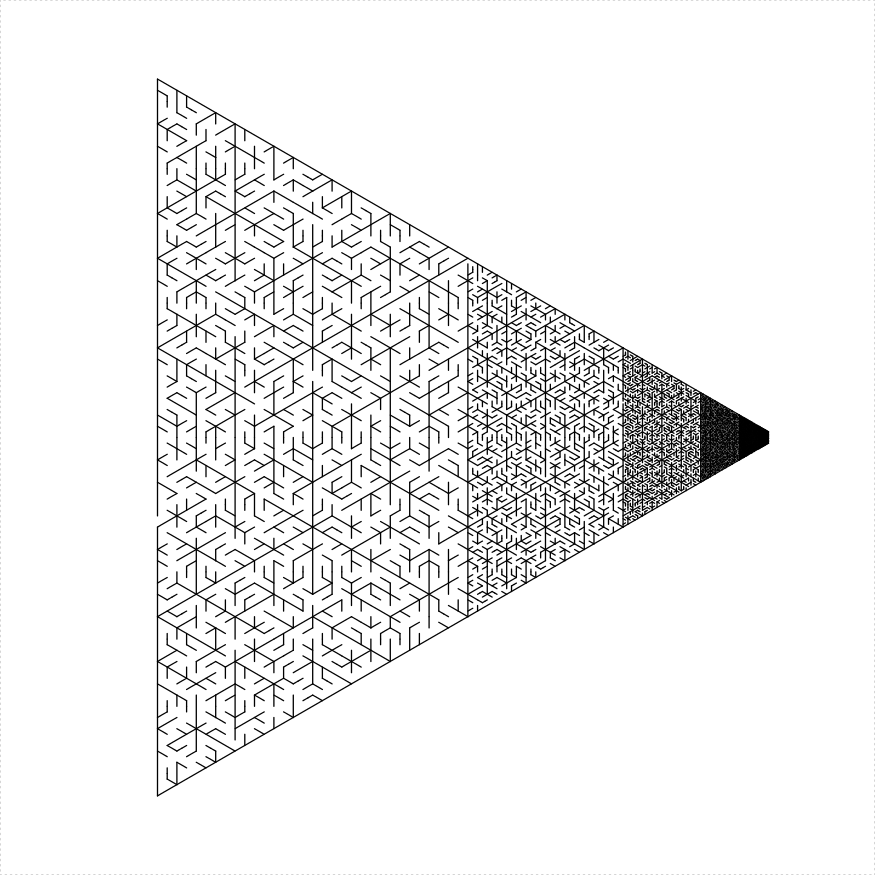
plot of chunk unit-len-stack-trap
The parameters draw_boundary,
boundary_lines, boundary_holes,
num_boundary_holes and boundary_hole_color
control the drawing of the final outer boundary of polynomial mazes.
Without a boundary the maze can be used in recursive construction.
Adding a boundary provides the typical entry and exit points of a maze.
The parameter draw_boundary is a single Boolean that
controls whether the boundary is drawn or not. The parameter
boundary_lines may be a scalar Boolean, or a numeric array
giving the indices of which sides should have drawn boundary lines. The
sides are numbered in the order in which they appear, and are controlled
by the clockwise parameter. The parameter
boundary_holes is a numeric array giving the indices of the
boundary lines that should have holes. If NULL, then we
uniformly choose num_boundary_holes holes at random. Holes
can be drawn as colored segments with the
boundary_hole_color, which is a character array giving the
color of each hole. The value ‘clear’ stands in for clear holes.
library(TurtleGraphics)
library(mazealls)
# side by side
turtle_init(1000, 400)
turtle_up()
turtle_hide()
turtle_do({
turtle_left(90)
turtle_forward(distance = 450)
turtle_right(90)
parallelogram_maze(unit_len = 10, height = 25,
draw_boundary = FALSE, end_side = 3)
turtle_left(90)
turtle_forward(distance = 30)
turtle_left(90)
parallelogram_maze(unit_len = 10, height = 25,
draw_boundary = TRUE, boundary_lines = c(1,
3), boundary_holes = FALSE, end_side = 3)
turtle_left(90)
turtle_forward(distance = 30)
turtle_left(90)
parallelogram_maze(unit_len = 10, height = 25,
draw_boundary = TRUE, boundary_lines = c(2,
4), boundary_holes = c(2, 4), boundary_hole_color = c("ignore",
"green", "ignore", "blue"))
})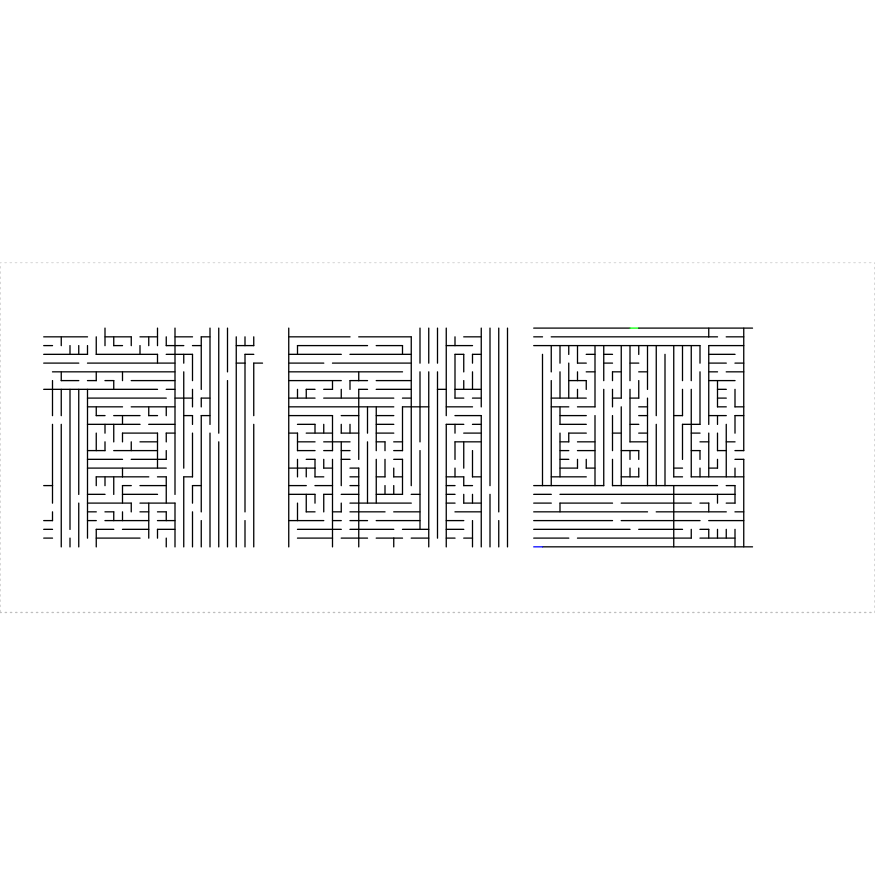
plot of chunk boundary-stuff
The end_side parameter controls which side of the maze
the turtle ends on. The default value of 1 essentially causes the turtle
to end where it started. The sides are numbered in the order in which
the boundary would be drawn. Along with the boundary controls, the
ending side can be useful to join together polygons into more complex
mazes, as below:
library(TurtleGraphics)
library(mazealls)
# triangle of hexes
turtle_init(2500, 2500)
turtle_up()
turtle_hide()
ul <- 22
dep <- 4
turtle_do({
turtle_left(90)
turtle_forward(distance = 1150)
turtle_right(90)
turtle_backward(distance = 650)
hexagon_maze(unit_len = ul, depth = dep, end_side = 4,
draw_boundary = TRUE, boundary_holes = c(1,
3, 4))
parallelogram_maze(unit_len = ul, height = 2^dep,
clockwise = FALSE, width = 3 * (2^dep), end_side = 3,
draw_boundary = TRUE, num_boundary_holes = 0,
boundary_lines = c(2, 4))
hexagon_maze(unit_len = ul, depth = dep, end_side = 2,
draw_boundary = TRUE, boundary_holes = c(1,
2))
parallelogram_maze(unit_len = ul, height = 2^dep,
clockwise = FALSE, width = 3 * (2^dep), end_side = 3,
draw_boundary = TRUE, num_boundary_holes = 0,
boundary_lines = c(2, 4))
hexagon_maze(unit_len = ul, depth = dep, end_side = 2,
draw_boundary = TRUE, boundary_holes = c(1,
5))
parallelogram_maze(unit_len = ul, height = 2^dep,
clockwise = FALSE, width = 3 * (2^dep), end_side = 3,
draw_boundary = TRUE, num_boundary_holes = 0,
boundary_lines = c(2, 4))
})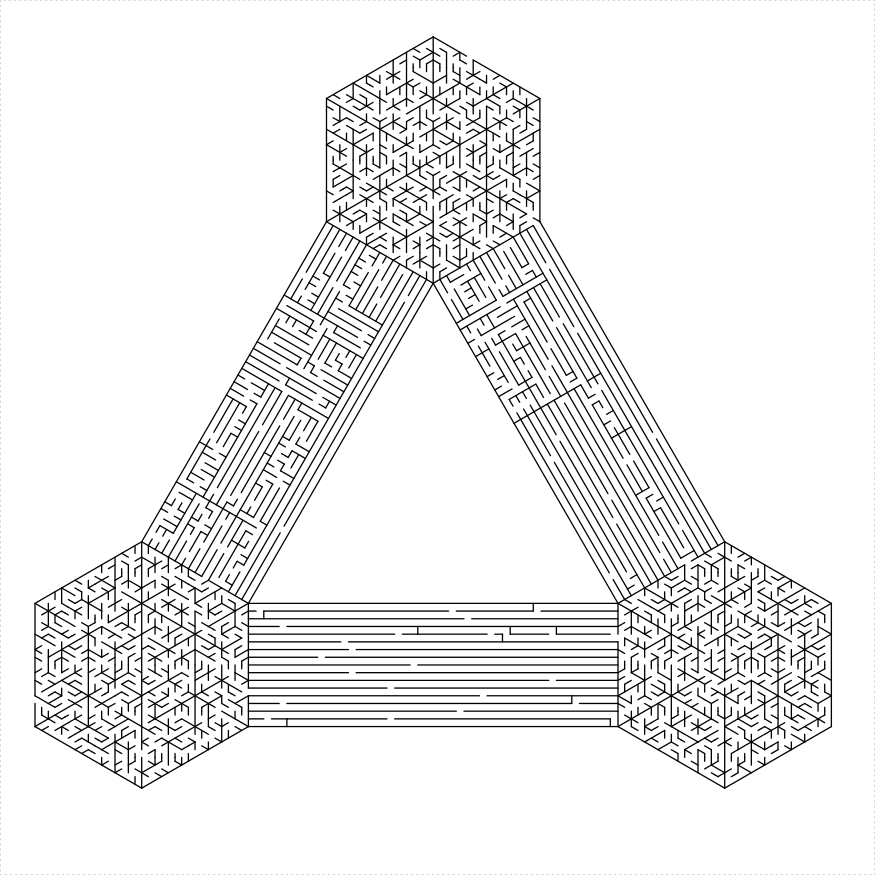
plot of chunk tri-of-hex
library(TurtleGraphics)
library(mazealls)
# tiling!
tile_bit <- function(unit_len, depth, clockwise = TRUE,
draw_boundary = FALSE, boundary_holes = NULL) {
turtle_col("black")
parallelogram_maze(unit_len = unit_len, height = 2^depth,
clockwise = clockwise, draw_boundary = TRUE,
num_boundary_holes = 4)
turtle_col("red")
for (iii in c(1:4)) {
turtle_forward(unit_len * 2^(depth - 1))
turtle_right(90)
turtle_forward(unit_len * 2^(depth - 1))
eq_triangle_maze(unit_len = unit_len, depth = depth,
clockwise = !clockwise, draw_boundary = draw_boundary,
boundary_lines = ifelse(iii <= 2, 2, 3),
num_boundary_holes = 3, end_side = ifelse(iii ==
4, 2, 1))
if (iii == 2) {
turtle_col("blue")
}
}
turtle_col("black")
if (draw_boundary) {
blines <- c(1, 2, 4)
} else {
blines = 1
}
parallelogram_maze(unit_len = unit_len, height = 2^depth,
clockwise = clockwise, draw_boundary = TRUE,
boundary_lines = blines, boundary_holes = blines,
end_side = 3)
turtle_forward(unit_len * 2^(depth - 1))
turtle_left(60)
turtle_forward(unit_len * 2^(depth - 1))
}
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
x0 <- 220
y0 <- 0
ul <- 20
dep <- 5
turtle_do({
for (jjj in c(1:5)) {
turtle_setpos(x = x0, y = y0)
turtle_setangle(angle = 0)
replicate(5, tile_bit(unit_len = ul, depth = dep,
draw_boundary = TRUE))
x0 <- x0 + ul * (2^dep) * (1 + sqrt(3)/2)
y0 <- y0 + ul * (2^(dep - 1))
}
})
plot of chunk tileit
Or whatever you call it. Here are some mazes built using the primitives.
Like it says on the label.
library(TurtleGraphics)
library(mazealls)
treeit <- function(unit_len, depth, height, left_shrink = 3/4,
right_shrink = 1/3) {
height <- ceiling(height)
parallelogram_maze(unit_len = unit_len, height = 2^depth,
width = height, clockwise = TRUE, draw_boundary = TRUE,
boundary_lines = c(1, 2, 4), start_from = "midpoint",
boundary_holes = c(1), end_side = 3)
if (depth > 0) {
iso_trapezoid_maze(depth = depth - 1, unit_len = unit_len,
clockwise = FALSE, draw_boundary = TRUE,
boundary_lines = c(1, 3), start_from = "midpoint",
boundary_holes = c(1), end_side = 4)
treeit(unit_len = unit_len, depth = depth -
1, height = left_shrink * height, left_shrink = left_shrink,
right_shrink = right_shrink)
turtle_right(180)
turtle_forward(unit_len * 2^(depth - 2))
turtle_right(60)
turtle_forward(unit_len * 2^(depth - 1))
turtle_right(60)
turtle_forward(unit_len * 2^(depth - 2))
turtle_right(180)
treeit(unit_len = unit_len, depth = depth -
1, height = right_shrink * height, left_shrink = left_shrink,
right_shrink = right_shrink)
turtle_forward(unit_len * 2^(depth - 2))
turtle_left(60)
turtle_forward(unit_len * 2^(depth - 2))
turtle_left(90)
turtle_forward(unit_len * sqrt(3) * 2^(depth -
2))
turtle_left(90)
}
turtle_right(90)
turtle_forward(unit_len * height)
turtle_right(90)
}
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(1600, 20)
turtle_setangle(270)
treeit(unit_len = 13, depth = 5, height = 70, left_shrink = 2/3,
right_shrink = 1/3)
})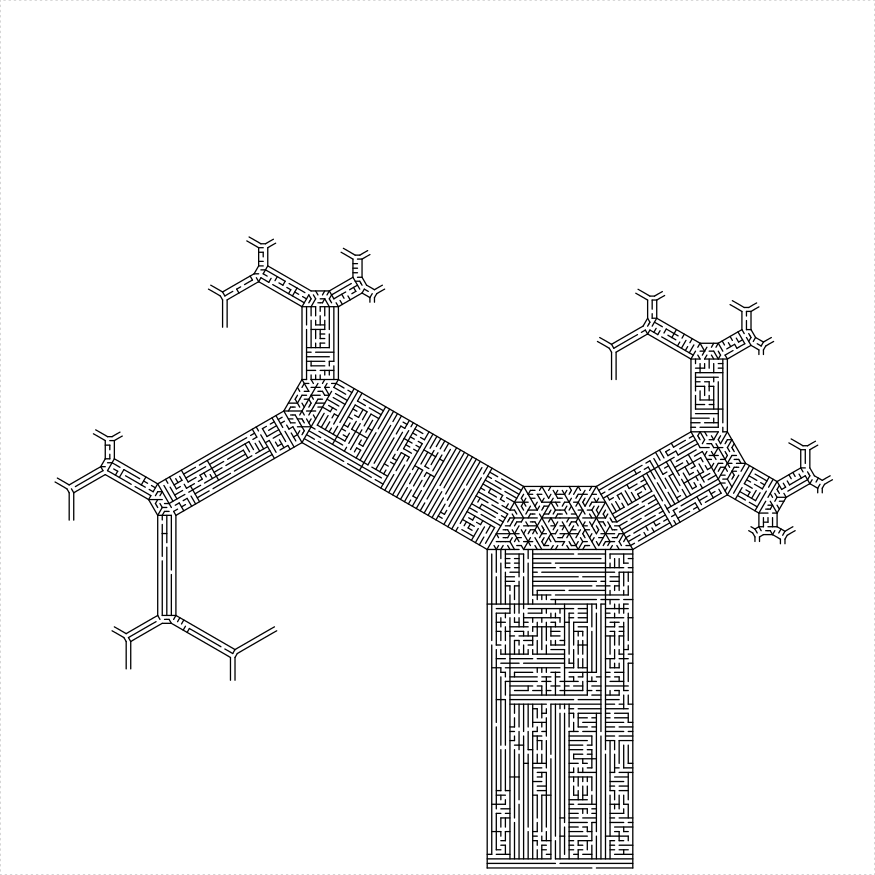
plot of chunk tree-thing
library(TurtleGraphics)
library(mazealls)
lwid <- 15
set.seed(1234)
turtle_init(1400, 1600, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_left(180)
turtle_forward(500)
turtle_left(90)
turtle_col("brown")
parallelogram_maze(angle = 90, unit_len = lwid,
width = 18, height = 16, method = "uniform",
boundary_lines = c(2, 3, 4), boundary_holes = c(3),
end_side = 1, draw_boundary = TRUE)
turtle_right(180)
turtle_col("green")
bigwid <- 42
for (iii in c(1:4)) {
if (iii == 1) {
bmid <- sample(bigwid + c(-3:3), 1)
} else {
bmid <- sample(bigwid + c(-8:8), 1)
}
iso_trapezoid_maze(depth = log2(bigwid), unit_len = lwid,
method = "one_ear", draw_boundary = TRUE,
boundary_lines = c(1, 2, 4), boundary_holes = c(1),
boundary_hole_locations = c(bmid, 0, 0,
0), end_side = 3)
bigwid <- 2 + (bigwid/2)
turtle_right(180)
}
eq_triangle_maze(depth = log2(2 * bigwid - 2),
unit_len = lwid, method = "stack_trapezoids",
draw_boundary = TRUE, boundary_lines = c(1,
2, 3), boundary_holes = c(1, 2), boundary_hole_locations = c(sample((bigwid) +
c(-3:3), 1), sample(10:50, 1), 0), end_side = 3)
})
plot of chunk christmas-tree
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
della <- -3
lens <- seq(from = 120, to = 2 - della, by = della)
ulen <- 10
high <- 14
turtle_do({
turtle_setpos(260, 570)
turtle_setangle(270)
for (iter in seq_along(lens)) {
parallelogram_maze(unit_len = ulen, height = high,
width = lens[iter], start_from = "corner",
clockwise = TRUE, draw_boundary = TRUE,
boundary_holes = c(1, 3), end_side = 3)
eq_triangle_maze(unit_len = ulen, depth = log2(high),
start_from = "corner", clockwise = FALSE,
draw_boundary = TRUE, boundary_lines = c(3),
num_boundary_holes = 0, boundary_holes = rep(FALSE,
3), end_side = 2)
}
parallelogram_maze(unit_len = ulen, height = high,
width = lens[iter] + della, start_from = "corner",
clockwise = TRUE, draw_boundary = TRUE, boundary_holes = c(1,
3), end_side = 3)
})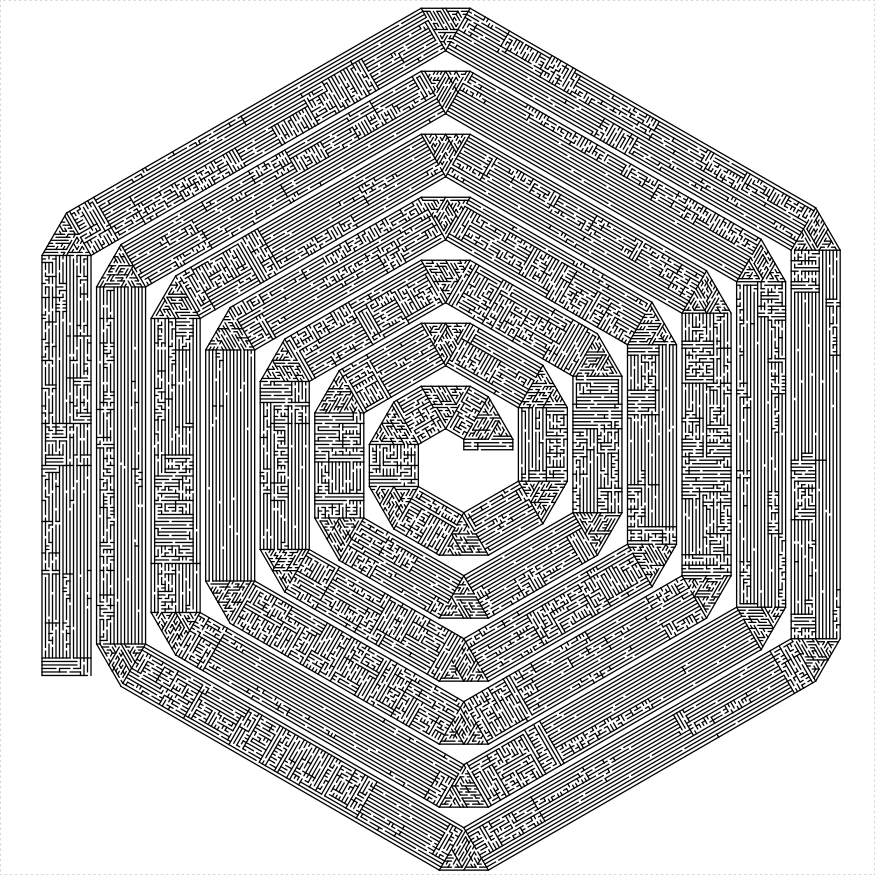
plot of chunk hex-spiral
Well, a rhombus spiral.
rect_spiral <- function(unit_len, height, width, thickness = 8L,
angle = 90, clockwise = TRUE, start_hole = FALSE) {
if (start_hole) {
bholes <- 1
fourl_dist <- height - thickness
} else {
bholes <- 4
fourl_dist <- height
}
last_one <- (width < thickness)
if (last_one) {
blines <- 1:4
bholes <- c(3, bholes)
} else {
blines <- c(1, 2, 4)
}
blocs <- -sample.int(n = thickness, size = 4, replace = TRUE)
parallelogram_maze(unit_len = unit_len, height = thickness,
width = fourl_dist, angle = 180 - angle, start_from = "corner",
clockwise = clockwise, draw_boundary = TRUE,
boundary_lines = blines, boundary_holes = bholes,
boundary_hole_locations = blocs, end_side = 3)
if (clockwise) {
turtle_left(angle)
} else {
turtle_right(angle)
}
if (!last_one) {
rect_spiral(unit_len, height = width, width = height -
thickness, thickness = thickness, angle = 180 -
angle, clockwise = clockwise, start_hole = FALSE)
}
}
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(300, 50)
turtle_setangle(270)
rect_spiral(unit_len = 20, 110, 90, thickness = 15,
angle = 80, start_hole = TRUE)
})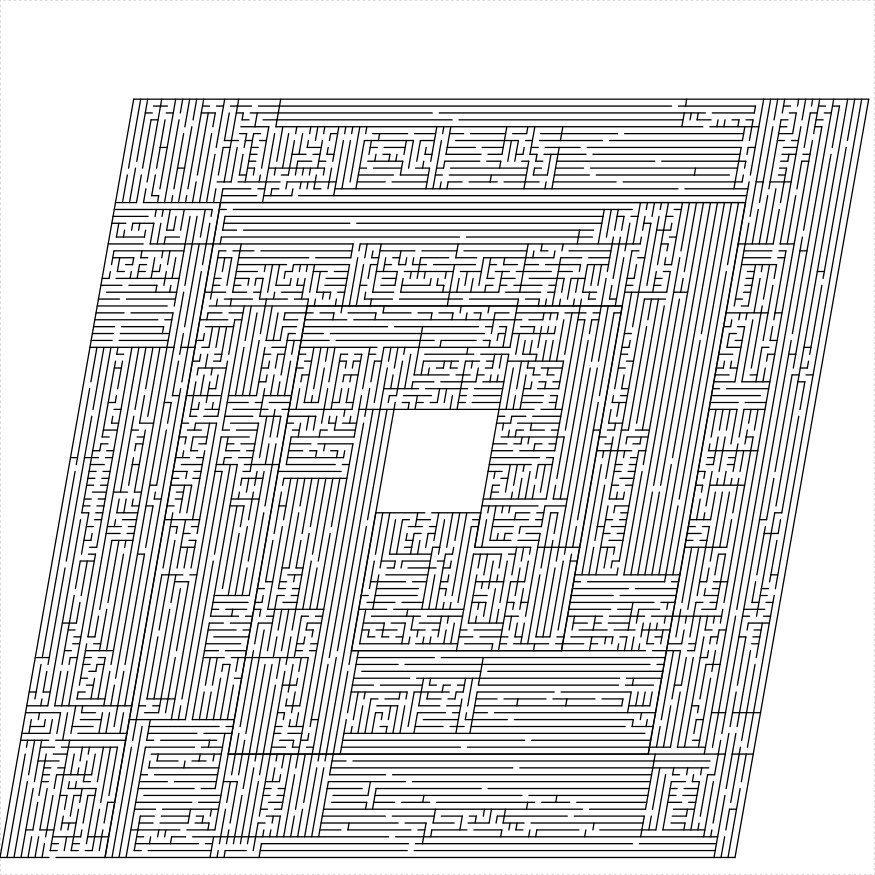
plot of chunk rect-spiral
The path spirals in, then out, joining at the center. This might be buggy.
double_spiral <- function(unit_len, height, width,
thickness = 8L, angle = 90, clockwise = TRUE, start_hole = TRUE,
color1 = "black", color2 = "black") {
len1 <- height - thickness
bline1 <- c(1, 2, 4)
bline2 <- c(1, 3, 4)
bhole1 <- c(2)
if (start_hole) {
len2 <- len1
bline2 <- c(bline2, 2)
bhole1 <- c(bhole1, 4)
} else {
len2 <- len1 - 2 * thickness
}
blocs1 <- -sample.int(n = thickness, size = 4,
replace = TRUE)
blocs2 <- -sample.int(n = thickness, size = 4,
replace = TRUE)
last_one <- (min(len1, len2) <= 0) || (width <=
2 * thickness)
if (last_one) {
bhole2 <- c(4)
} else {
bhole2 <- c(3)
}
if (start_hole) {
bhole2 <- c(bhole2, 2)
}
second_stripe <- ((len2 > 0) && (width > thickness))
if (len1 > 0) {
turtle_col(color1)
parallelogram_maze(unit_len = unit_len, height = len1,
width = thickness, angle = angle, start_from = "corner",
clockwise = clockwise, draw_boundary = TRUE,
boundary_lines = bline1, boundary_holes = bhole1,
boundary_hole_locations = blocs1, end_side = ifelse(len2 >
0, 3, 2))
if (second_stripe) {
wid2 <- min(thickness, width - thickness)
turtle_col(color2)
parallelogram_maze(unit_len = unit_len,
height = len2, width = wid2, angle = 180 -
angle, start_from = "corner", clockwise = !clockwise,
draw_boundary = TRUE, boundary_lines = bline2,
boundary_holes = bhole2, boundary_hole_locations = blocs2,
end_side = 4)
turtle_col(color1)
turtle_forward(unit_len * (thickness +
wid2))
if (clockwise) {
turtle_right(180 - angle)
} else {
turtle_left(180 - angle)
}
turtle_forward(unit_len * thickness)
if (clockwise) {
turtle_right(angle)
} else {
turtle_left(angle)
}
}
}
next_height <- width
next_width <- ifelse(start_hole, height, height -
2 * thickness)
if (last_one) {
if (second_stripe) {
parallelogram_maze(unit_len = unit_len,
height = next_height, width = thickness,
start_from = "corner", angle = 180 -
angle, clockwise = clockwise)
} else {
parallelogram_maze(unit_len = unit_len,
height = next_height, width = thickness,
start_from = "corner", angle = angle,
clockwise = !clockwise)
}
} else {
double_spiral(unit_len, height = next_height,
width = next_width, thickness = thickness,
angle = 180 - angle, clockwise = clockwise,
start_hole = FALSE, color1 = color1, color2 = color2)
}
}
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(300, 50)
turtle_setangle(0)
double_spiral(unit_len = 20, height = 100, width = 100,
thickness = 10, angle = 80, start_hole = TRUE,
color2 = "gray40")
})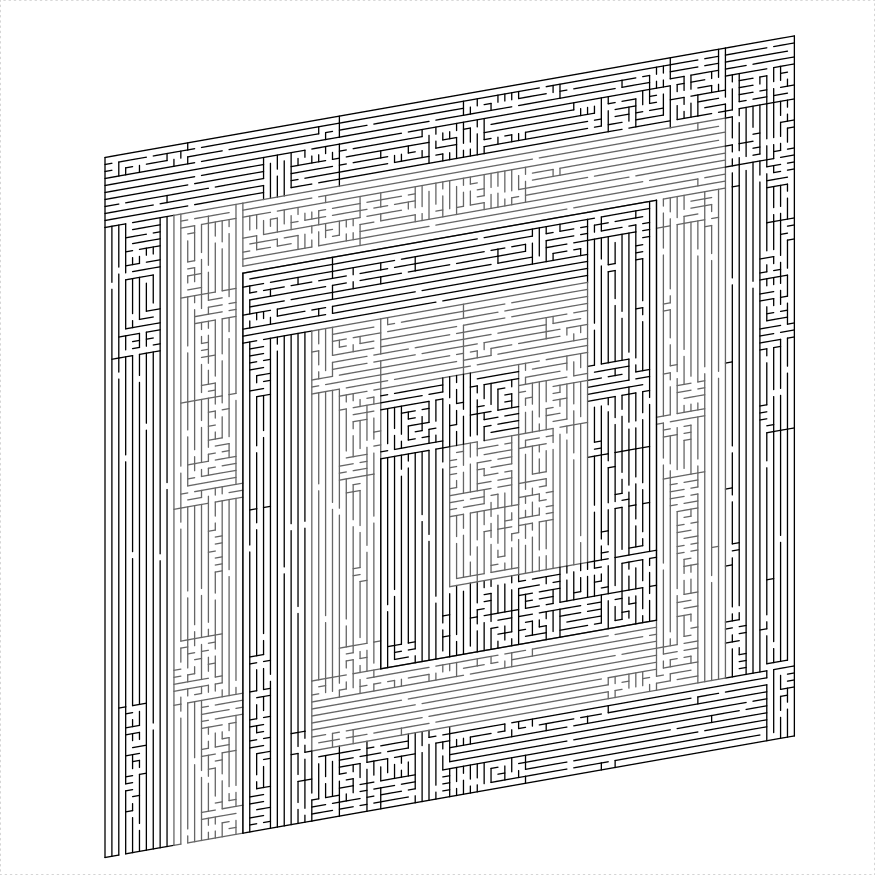
plot of chunk rect-double-spiral
As in ox that plods back and forth in a field.
boustro <- function(unit_len, height, width, thickness = 8L,
angle = 90, clockwise = TRUE, start_hole = TRUE,
balance = 0) {
if (start_hole) {
bholes <- c(1, 3)
blines <- 1:4
} else {
bholes <- c(1, 3)
blines <- 2:4
}
last_one <- (width < thickness)
blocs <- sample.int(n = thickness, size = 4, replace = TRUE)
parallelogram_maze(unit_len = unit_len, height = height,
width = thickness, angle = angle, balance = balance,
start_from = "corner", clockwise = clockwise,
draw_boundary = TRUE, boundary_lines = blines,
boundary_holes = bholes, boundary_hole_locations = blocs,
end_side = 3)
if (!last_one) {
boustro(unit_len, height = height, width = width -
thickness, thickness = thickness, angle = 180 -
angle, clockwise = !clockwise, start_hole = FALSE,
balance = balance)
}
}
turtle_init(2500, 2500, mode = "clip")
turtle_up()
turtle_hide()
turtle_do({
turtle_setpos(100, 50)
turtle_setangle(0)
boustro(unit_len = 26, height = 82, width = 80,
thickness = 8, angle = 85, balance = 1.5)
})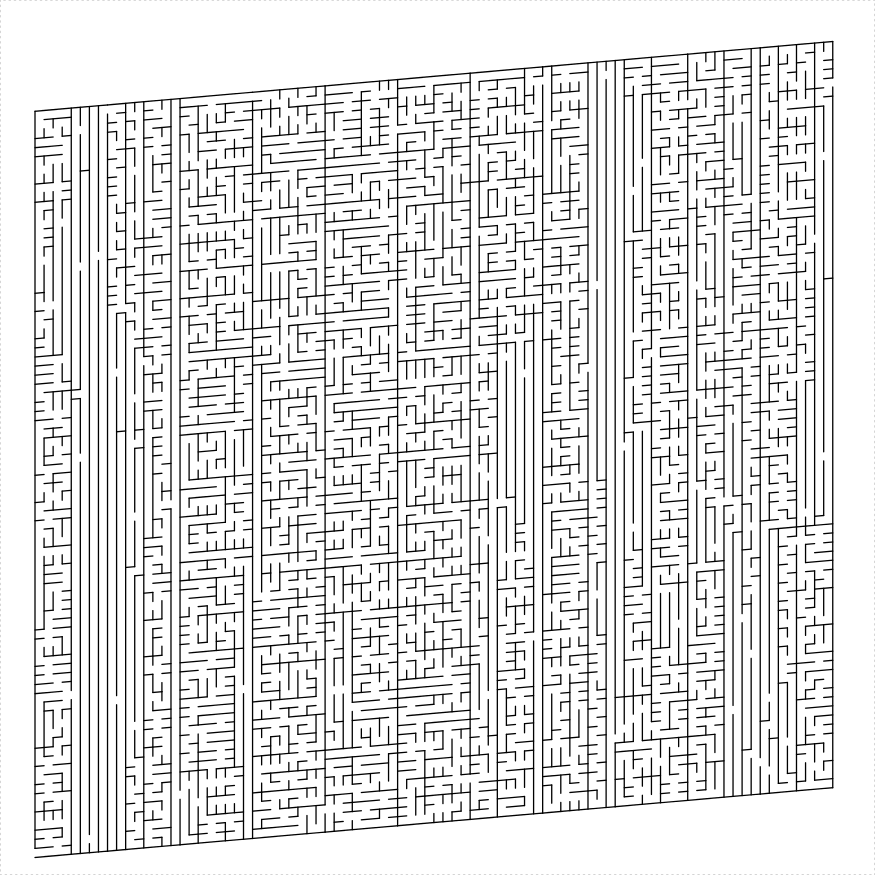
plot of chunk rect-boustrophedon